Jak zamieniasz sześcian w kulę?

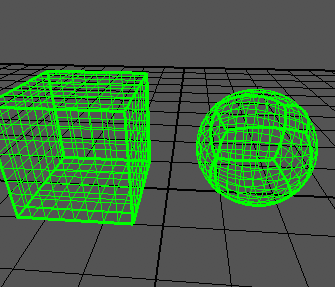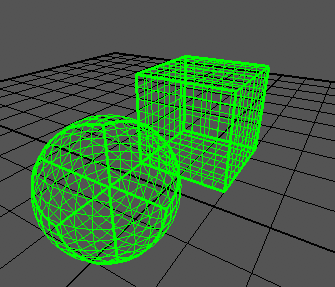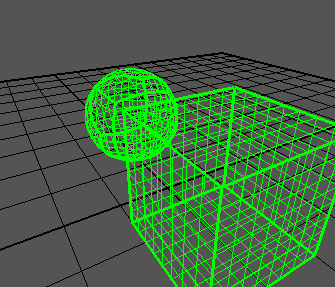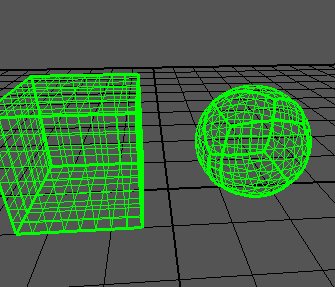
Próbuję stworzyć quad-kulę na podstawie artykułu , który pokazuje takie wyniki:

Mogę poprawnie wygenerować kostkę:

Ale kiedy przekonwertuję wszystkie punkty zgodnie z tym wzorem (ze strony, do której prowadzi link powyżej):

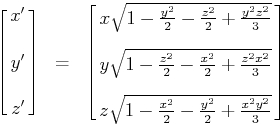
    x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
    y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
    z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Moja kula wygląda następująco:

Jak widać, krawędzie sześcianu wciąż wystają zbyt daleko. Sześcian rozciąga się od -1do +1we wszystkich osiach, jak mówi artykuł.

Jakieś pomysły, co jest nie tak?

Źle napisałeś formułę.

x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Zmieniasz oryginał xi zastępujesz go. Następnie modyfikujesz ynie w oparciu o oryginał, xale zmodyfikowany x. Następnie modyfikujesz zna podstawie zmodyfikowanej wersji obu tych elementów.

Zachowaj oryginały i oblicz to:

float dx = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0));
float dy = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0));
float dz = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Od tego momentu używaj dx, dy i dz.