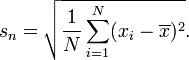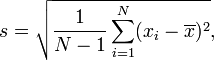Dlaczego szkoły amerykańskie i brytyjskie uczą różnych metod obliczania odchylenia standardowego?

15

Jak rozumiem, brytyjskie szkoły uczą, że odchylenie standardowe można znaleźć za pomocą:

$alternatywny tekst$

mając na uwadze, że szkoły amerykańskie uczą:

$alternatywny tekst$

(w każdym razie na poziomie podstawowym).

W przeszłości powodowało to problemy wielu moich studentów, którzy szukali w Internecie, ale znaleźli złe wyjaśnienie.

Skąd ta różnica?

Przy prostych zestawach danych powiedz 10 wartości, jaki będzie błąd, jeśli zastosowana zostanie niewłaściwa metoda (np. Podczas egzaminu)?

— Amos
źródło

4

Nie jestem pewien, czy scharakteryzowanie jednej lub drugiej jako „złej” formuły jest sposobem na zrozumienie problemu. Tyle tylko, że drugi jest „lepszy” w tym sensie, że jest obiektywnym estymatorem prawdziwego odchylenia standardowego. Jeśli więc zależy Ci na obiektywnych szacunkach, drugi jest „lepszy” / „poprawny”.

Charakteryzowałem tę formułę jako „złą” wyłącznie w tym sensie, że na egzaminie, jeśli użyjesz formuły, która nie jest zakazana w sylabusie, skończysz na „złej” odpowiedzi. Plus, jeśli wartości nie są próbą populacji per se, to z pewnością pierwsza formuła daje dokładniejszą wartość.

— Amos,

14

Srikant, nie sądzę, aby ten drugi był obiektywnym estymatorem. Kwadrat jest bezstronnym estymatorem prawdziwej wariancji. Jednak Nierówność Jensena ustala, że oczekiwanie funkcji krzywoliniowej zmiennej losowej nie jest takie samo, jak funkcji oczekiwania zmiennej losowej. Dlatego druga formuła nie może być bezstronnym estymatorem prawdziwego odchylenia standardowego.

— Andrew Robinson,

Dla porównania: został również zapytany @ m.SE ...

— JM nie jest statystykiem

4

Każda szkoła z nami za pomocą bardzo popularny elementarną tekstu przez Freedman, Pisani, i Purves jest za pomocą pierwszego wzoru (

), więc wydaje się niewłaściwe, aby scharakteryzować to jako US vs. Brytanii różnicy.

s_{n}

$s_n$

— whuber

18

Pierwszy wzór to odchylenie standardowe populacji, a drugi wzór to odchylenie standardowe próbki . Druga formuła jest również związana z bezstronnym estymatorem wariancji - więcej informacji można znaleźć w Wikipedii .

Przypuszczam (tutaj) w Wielkiej Brytanii, że nie dokonują rozróżnienia między próbą a populacją w szkole średniej. Z pewnością nie dotykają takich pojęć, jak stronnicze estymatory.

— csgillespie
źródło

4

Colin, bezstronny estymator odchylenia standardowego, nie ma zamkniętego przedstawienia formy w ogólnym przypadku. Istnieje obiektywny estymator wariancji (w tym przypadku s 2 ). Warto zauważyć, że oba są spójnymi estymatorami wariancji populacji - a więc przez twierdzenie o ciągłym odwzorowaniu są dwoma estymatorami odchyleń standardowych. Powiązaną kwestią jest to, że s n 2 ma niższy MSE niż s 2 . Dodatkowa korzyść wynikająca z narzucania bezstronności jest dyskusyjna.

— Mornington

@Tirthankar - bardzo niechlujny ze mnie. Lekko zmieniłem odpowiedź. Dzięki.

— csgillespie

2

O ile pamiętam, uczono mnie obliczeń „próbnych” w matematyce i naukach ścisłych GCSE (w wieku 14–16 lat), a rozróżnienie między populacjami i próbkami oraz powiązanych miar wariancji zostało uwzględnione (choć nie dogłębnie) na poziomie A ( 16-18 lat). Nie jestem więc pewien, czy to prosta różnica między Wielką Brytanią a Stanami Zjednoczonymi.

— Freya Harrison

11

Ponieważ nikt jeszcze nie odpowiedział na ostatnie pytanie - a mianowicie, aby obliczyć różnice między dwiema formułami - zajmijmy się tym.

Z wielu powodów należy porównać odchylenia standardowe pod względem ich współczynników, a nie różnic. Stosunek wynosi

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

Przybliżenie może być postrzegane jako obcięcie (naprzemiennej) serii Taylora dla pierwiastka kwadratowego, wskazując, że błąd nie może przekroczyć =. To ustanawia, że przybliżenie jest więcej niż wystarczające (dla naszych celów) po $|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ wynosi lub więcej. $2$

Natychmiastowe jest, że dwa oszacowania SD są w granicach (około) 10% od siebie, gdy przekroczy , w granicach 5%, gdy przekroczy $N$ $5$ $N$ , i tak dalej. Oczywiście, dla wielu celów rozbieżności te są tak małe, że nie ma znaczenia, która formuła zostanie zastosowana, szczególnie gdy SD ma na celuopisanierozprzestrzeniania się danych lub dokonywaniepółilościowychocen lub prognoz (np. Przy zastosowaniu 68-95 -99.7 zasada kciuka). Rozbieżności są nawet mniej ważne przyporównywaniu $10$ SD, na przykład przy porównywaniu rozkładów dwóch zestawów danych. (Gdy zestawy danych są równe, rozbieżności faktycznie zanikają całkowicie, a obie formuły prowadzą do identycznych wniosków.) Prawdopodobnie są to formy rozumowania, których staramy się nauczyć początkujących uczniów, więc jeśli uczniowie zastanawiają się, jakiej formuły użyć, można to uznać za znak, że tekst lub klasa nie podkreśla tego, co jest naprawdę ważne.

$N$ $t$ $z$ $s$ $s_n$

— Whuber
źródło

6

To jest Korekta Bessela . Wersja amerykańska pokazuje wzór na odchylenie standardowe próbki , przy czym wersja brytyjska powyżej jest odchyleniem standardowym próbki .

— Reed Copsey
źródło

5

Nie jestem pewien, czy jest to kwestia czysto amerykańsko-brytyjska. Reszta tej strony została zaczerpnięta z napisanego przeze mnie FAQ. ( Http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Jak obliczyć SD z n-1 w mianowniku

Oblicz kwadrat różnicy między każdą wartością a średnią próbki.
Dodaj te wartości.
Podziel sumę przez n-1. Wynik nazywa się wariancją.
Weź pierwiastek kwadratowy, aby uzyskać odchylenie standardowe.

Dlaczego n-1?

Dlaczego warto dzielić przez n-1 zamiast n, obliczając odchylenie standardowe? W kroku 1 obliczasz różnicę między każdą wartością a średnią z tych wartości. Nie znasz prawdziwego środka populacji; wszystko co wiesz to średnia z twojej próbki. Z wyjątkiem rzadkich przypadków, w których średnia próby okazuje się równa średniej populacji, dane będą bliższe średniej próby, niż rzeczywistej średniej populacji. Tak więc wartość obliczona w kroku 2 będzie prawdopodobnie nieco mniejsza (i nie może być większa) niż to, co byłoby, gdybyś użył prawdziwej populacji w kroku 1. Aby to zrekompensować, podziel przez n-1 niż nv Nazywa się to korektą Bessela.

Ale dlaczego n-1? Jeśli znasz średnią próbki i wszystkie wartości oprócz jednej, możesz obliczyć, jaka musi być ta ostatnia wartość. Statystycy twierdzą, że istnieje n-1 stopni swobody.

Kiedy SD należy obliczyć mianownikiem n zamiast n-1?

Książki statystyczne często pokazują dwa równania do obliczenia SD, jedno za pomocą n, a drugie za pomocą n-1 w mianowniku. Niektóre kalkulatory mają dwa przyciski.

Równanie n-1 jest używane w typowej sytuacji, w której analizujesz próbkę danych i chcesz wyciągnąć bardziej ogólne wnioski. Obliczona w ten sposób SD (z n-1 w mianowniku) najlepiej zgaduje wartość SD w całej populacji.

Jeśli chcesz po prostu skwantyfikować zmienność określonego zestawu danych i nie planujesz ekstrapolować, aby wyciągnąć szersze wnioski, możesz obliczyć SD, używając n w mianowniku. Wynikowa SD to SD tych konkretnych wartości. Obliczanie SD w ten sposób nie ma sensu, jeśli chcesz oszacować SD populacji, z której te punkty zostały wyciągnięte. Zastosowanie n w mianowniku ma sens tylko wtedy, gdy nie pobiera się próbek z populacji, nie ma potrzeby wyciągania ogólnych wniosków.

Celem nauki jest prawie zawsze uogólnienie, więc nie należy stosować równania z mianownikiem. Jedynym przykładem, jaki mogę wymyślić, gdzie to ma sens, jest kwantyfikacja zróżnicowania wyników egzaminów. Ale znacznie lepiej byłoby pokazać wykres punktowy każdego wyniku lub histogram rozkładu częstotliwości.

— Harvey Motulsky
źródło

1

Nie sugerowałem, że tak, byłem po prostu ciekawy, dlaczego taka różnica mogła powstać, jaki poziom błędu wynikający z niewłaściwej porady może dać i czy istnieje dobre wyjaśnienie różnicy, którą mógłbym dać moim studentom .

— Amos,

@harvey - link nie działa

— baxx

1

@baxx .. Dziękujemy za zwrócenie na to uwagi. Naprawiony.

— Harvey Motulsky

3

Ponieważ N jest liczbą punktów w zbiorze danych, można argumentować, że obliczając średnią, zmniejszyliśmy stopień swobody w zbiorze danych o jeden (ponieważ wprowadzono zależność do zbioru danych), więc należy użyć N -1 przy szacowaniu odchylenia standardowego od zbioru danych, dla którego wcześniej trzeba było oszacować średnią.

— Benjamin Bannier
źródło