Zakładając, że zmienne są dodatnie lub nieujemne, krawędzie krawędzi są tylko punktami, powyżej których dane stałyby się odpowiednio 0 lub ujemne. Ponieważ takie rzeczywiste dane są zwykle wypaczone, widzimy większą gęstość punktów na dolnym końcu ich rozkładu, a zatem większą gęstość w „punkcie” klina.
Mówiąc bardziej ogólnie, PCA to po prostu obrót danych, a ograniczenia na tych danych będą ogólnie widoczne w głównych składnikach w taki sam sposób, jak pokazano w pytaniu.
Oto przykład wykorzystujący kilka zmiennych logarytmicznych o rozkładzie normalnym:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

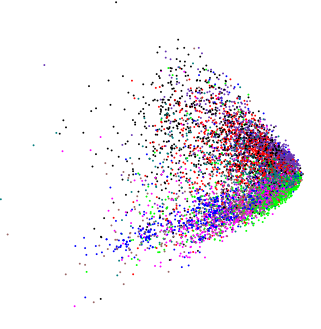
W zależności od rotacji sugerowanej przez dwa pierwsze komputery PC możesz zobaczyć klin lub nieco inną wersję, pokazaną tutaj w 3D za pomocą ( ordirgl()zamiast plot())

Tutaj w 3d widzimy wiele kolców wystających z masy centralnej.
Dla losowych zmiennych Gaussa (Xja∼ ( N) ( μ = 0 , σ= 1 )), gdzie każdy ma tę samą średnią i wariancję, widzimy sferę punktów
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


A dla jednolitych dodatnich zmiennych losowych widzimy sześcian
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


Zauważ, że tutaj dla ilustracji pokazuję mundur używając tylko 3 zmiennych losowych, stąd punkty opisują sześcian w 3d. Przy wyższych wymiarach / większej liczbie zmiennych nie możemy idealnie przedstawić hipersześcianu 5d w 3d, a zatem wyraźny kształt „sześcianu” ulega nieco zniekształceniu. Podobne problemy wpływają na inne pokazane przykłady, ale nadal łatwo zauważyć ograniczenia w tych przykładach.
Dla twoich danych transformacja logiczna zmiennych przed PCA pociągnie za sobą ogony i rozciągnie zbite dane, tak jak możesz użyć takiej transformacji w regresji liniowej.
Inne kształty mogą pojawiać się na wykresach PCA; jeden taki kształt jest artefaktem reprezentacji metrycznej zachowanym w PCA i jest znany jako podkowa . W przypadku danych o długim lub dominującym gradiencie (próbki ułożone wzdłuż jednego wymiaru ze zmiennymi zwiększającymi się od 0 do maksimum, a następnie zmniejszającymi się ponownie do 0 wzdłuż części danych, są dobrze znane z generowania takich artefaktów.
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

co tworzy ekstremalną podkowę, w której punkty na końcach osi wyginają się z powrotem w środek.

 .
. (z wyjątkiem tego przypadku naprawdę chciałem wiedzieć, czy jest jakaś struktura wewnętrzna).
(z wyjątkiem tego przypadku naprawdę chciałem wiedzieć, czy jest jakaś struktura wewnętrzna).






