To pytanie wynika z mojego faktycznego zamieszania dotyczącego tego, jak zdecydować, czy model logistyczny jest wystarczająco dobry. Mam modele, które wykorzystują stan par projekt indywidualny dwa lata po ich uformowaniu jako zmienna zależna. Wynik jest udany (1) lub nie (0). Mam zmienne niezależne mierzone w czasie tworzenia par. Moim celem jest sprawdzenie, czy zmienna, która, jak podejrzewałem, wpłynie na sukces par, ma wpływ na ten sukces, kontrolując inne potencjalne wpływy. W modelach zmienna zainteresowania jest znacząca.
Modele oszacowano za pomocą glm()funkcji w R. Aby ocenić jakość modeli, zrobiłem kilka rzeczy: domyślnie glm()daje ci residual deviance, the AICi BIC. Ponadto obliczyłem poziom błędu modelu i narysowałem skumulowane reszty.
- Kompletny model ma mniejsze odchylenie resztkowe, AIC i BIC niż inne modele, które oszacowałem (i które są zagnieżdżone w pełnym modelu), co prowadzi mnie do wniosku, że ten model jest „lepszy” niż inne.
- Wskaźnik błędu modelu jest dość niski, IMHO (jak w Gelman i Hill, 2007, s. 99 ):
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1)około 20%.
Jak na razie dobrze. Ale kiedy planuję resztki bin (ponownie zgodnie z radami Gelmana i Hilla), duża część pojemników nie mieści się w 95% CI:
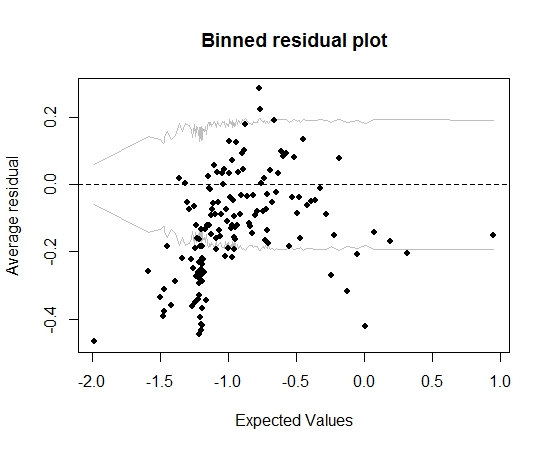
Ta fabuła prowadzi mnie do wniosku, że w modelu jest coś zupełnie nie tak. Czy to powinno doprowadzić mnie do wyrzucenia modelu? Czy powinienem uznać, że model jest niedoskonały, ale zachować go i zinterpretować efekt zmiennej zainteresowania? Bawiłem się z wykluczaniem z kolei zmiennych, a także pewną transformacją, bez poprawiania wykresu binned residuals.
Edytować:
- W tej chwili model ma kilkanaście predyktorów i 5 efektów interakcji.
- Pary są „względnie” niezależne od siebie w tym sensie, że wszystkie powstają w krótkim okresie czasu (ale nie ściśle mówiąc, wszystkie jednocześnie) i istnieje wiele projektów (13 tys.) I wiele osób (19 tys. ), więc do sporej części projektów dołącza tylko jedna osoba (istnieje około 20000 par).