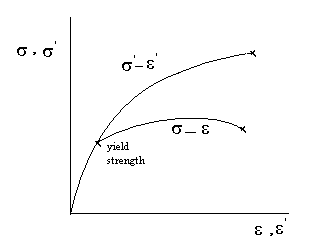Dlaczego w ogóle używamy stresu technicznego?

Zaskakujące, że nie zostało to wcześniej zadane, więc muszę przegapić coś prostego.

W tym eq używamy stresu inżynieryjnego i obciążenia technicznego. Naprężenie = (moduł Younga) × (odkształcenie). Ten ekw. służy do analizy gięcia belek, skręcania wałów i wyboczenia. Tak więc końcowe równanie zginania i skręcania da nam wartość stresu inżynieryjnego, ale nie wartość stresu.$(\frac{M}{I} = \frac{\sigma}{y})$$(\frac{T}{I} = \frac{\tau}{r})$

Dlaczego rozważamy stres techniczny zamiast prawdziwego stresu, skoro wiemy, że nie da on prawidłowej wartości stresu?

Niektóre rzeczy, które czytam to:

1. Trudne do zmierzenia.
2. Niewielka różnica, a my możemy zastosować współczynnik bezpieczeństwa.
3. „Nie uważamy, aby materiały zmieniały pole przekroju po obciążeniu, ponieważ projektujemy, aby nie ulegać odkształceniu plastycznemu, obszar elastyczny jest najważniejszy, dlatego to, co dzieje się po granicy proporcjonalności, nie jest ważne”

Po pierwsze, 1 i 2 nie są dla mnie prawdziwymi powodami. Liczba 3 wydaje się prawdopodobna, ponieważ zawsze projektujemy w obszarze elastycznym, ale czy to jest to? Czy obciążenie inżynieryjne dostarcza nawet ważnych informacji po ograniczeniu proporcjonalnym?

Używamy odkształcenia technicznego, nawet jeśli nie jest to „poprawna” wartość, ponieważ w większości przypadków, szczególnie w reżimie sprężystym, odkształcenie techniczne nieznacznie różni się od odkształcenia rzeczywistego.

W przypadku liniowych materiałów elastycznych typu Hookean na ogół odkształcenie przy granicy sprężystości jest bardzo małe. Na przykład nawet najsilniejsze stale mają górną granicę, gdy obrabiano na zimno około . Moduł stali wynosi około . Zatem dla najsilniejszych stali. Na początku odkształcenia plastycznego odkształcenie techniczne wynosi . Wiele użytecznych materiałów elastycznych ma znacznie niższe naprężenia konstrukcyjne w swoich granicach sprężystości. E = 200 × 10 9 Pa ε el = 0,005 = 0,5 % 0,5 $\sigma_{\textrm{el}}=1\times 10^{9}\ \textrm{Pa}$$E=200\times 10^{9}\ \textrm{Pa}$$\varepsilon_{\textrm{el}}=0.005=0.5\%$$0.5\%$

W przypadku izotropowej, elastycznej bryły Hookean, spełnione są następujące warunki

$$\varepsilon_{x_{1}} = \frac{1}{E}\left[\sigma_{x_{1}}-\nu\left(\sigma_{x_{2}}+\sigma_{x_{3}}\right)\right]$$

bez utraty ogólności w wyborze . Zatem w jednoosiowym napięciu na granicy sprężystości zakładając, że materiał może się swobodnie kurczyć. Zatem . Ponieważ współczynnik Poissona wynosi około 0,3 dla stali w reżimie sprężystym, liniowe odkształcenie ściskające wynosi . Pole przekroju na granicy sprężystości wynosi zatem lub jest bardzo bliskie krotności pierwotnego obszaru.$x_{i}$$\sigma_{x_{2}}=\sigma_{x_{3}}=0$$\varepsilon_{x_{2}}=\varepsilon_{x_{3}}=-\frac{\sigma_{\textrm{el}}\nu}{E}=-\nu\varepsilon_{\textrm{el}}$$\nu$$0.0015$$(1-0.0015)^{2}A_{0}$$0.997$

Zatem rzeczywiste odkształcenie jest razy większe niż odkształcenie konstrukcyjne na granicy sprężystości lub około razy lub około większe. Należy pamiętać, że jest to granica elastyczności wyjątkowo silnego liniowo elastycznego materiału, a zatem rozsądnie zachowawcza ocena różnicy między rzeczywistym odkształceniem a odkształceniem technicznym w reżimie sprężystym.$\frac{1}{0.997}$$1.003$$0.3\%$

Chociaż powyższa analiza jest dość użyteczna w przypadku liniowo elastycznych ciał stałych Hookean, nie jest tak dobra w przypadku polimerów i materiałów biologicznych. Takie materiały są zwykle lepkosprężyste (lub całkowicie inną klasą materiału), a zatem zachowują się inaczej. Prawdziwy szczep również dość dziko odbiega od szczepu inżynieryjnego w reżimie plastycznym, o czym świadczy poniższy wykres ( tutaj )

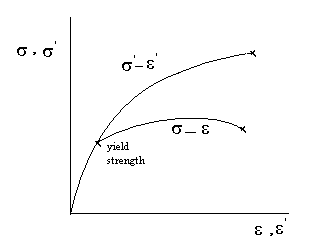
Co do twoich punktów:

1. Pomiar zmian w polu przekroju podczas deformacji jest trudny. Wymaga starannego umieszczenia skalibrowanego oprzyrządowania na precyzyjnie obrobionych próbkach testowych. Można użyć tensometrów umieszczonych po bokach pręta do rozciągania, aby zmierzyć naprężenie boczne w jednoosiowym napięciu i ściskaniu w urządzeniach do próby rozciągania . Uzyskanie statystycznie znaczących wyników wymaga wielu próbek, a także znacznego czasu, wysiłku i kosztów.

2. Jest to niewielka różnica. Mam nadzieję, że odpowiednio wyjaśniłem powyżej, jak mała jest różnica: w przypadku zachowawczym obliczyłem różnicę około .$0.3\%$

3. Pomysł, że możemy zignorować wszystko poza końcem elastycznego reżimu lub że zawsze projektujemy dla elastycznego reżimu, nie jest prawdziwy. Często warto badać odkształcenie plastyczne. Modelowanie ciągłych procesów kształtowania kształtów, takich jak walcowanie, ciągnienie, wytłaczanie itp., Wymaga dogłębnego zrozumienia mechaniki odkształcania plastycznego, aby zapewnić powodzenie, w tym celu prawdziwe naprężenie i prawdziwe odkształcenie są nieocenione. W szczególności do rysowania drutu, patrz (ten plik pdf ) i znajdź równanie 7. Deformacja plastyczna jest również przydatna do modelowania materiałów, które muszą trwale odkształcić się w niektórych spodziewanych przypadkach użytkowania, takich jak panele karoserii i elementy ramy podczas kolizji. Odkształcenie plastyczne jest przydatne, ponieważ pochłania energię kinetyczną.

Edycja: przepraszam, właściwie nie odpowiedziałem na stres. Jednak powinno być dość jasne, że te same punkty dotyczą naprężenia, co odnoszą się do odkształcenia, biorąc pod uwagę ich liniową zależność w systemie sprężystym. Ponownie, w reżimie plastikowym mogą występować duże różnice.

Dodanie do odpowiedzi @ starrise:

Jeśli chodzi o odrzucenie powodów 1 i 2, zapominasz o analizie dotyczącej ich kosztów i korzyści. Jak pokazał @starrise w swojej odpowiedzi, różnica zwykle nie jest znacząca (chociaż inne materiały zwykle będą miały większe różnice).

$\pm6\%$ $\pm15\%$

Jaki jest więc sens rozważenia prawdziwego obciążenia w codziennej praktyce inżynierskiej, jeśli wszystkie inne właściwości (w tym granica plastyczności i wymiary przekroju) będą miały przypadkowe fluktuacje, które z pewnością zagłuszą „błąd” z powodu użycia szczep inżynieryjny zamiast prawdziwego szczepu?