Na pytanie „czym jest impedancja” chciałbym zauważyć, że impedancja jest szeroką koncepcją fizyki, której impedancja elektryczna jest tylko jednym przykładem.
Aby zrozumieć, co to znaczy i jak to działa, często łatwiej jest zamiast tego rozważyć impedancję mechaniczną. Pomyśl o pchaniu (przesuwaniu) ciężkiej kanapy po podłodze.
Przykładasz pewną siłę, a kanapa ślizga się z określoną prędkością, w zależności od tego, jak mocno naciskasz, ciężaru kanapy, rodzaju powierzchni podłogi, rodzaju stóp, jakie ma kanapa i tak dalej. W tej sytuacji możliwe jest zdefiniowanie impedancji mechanicznej, która daje stosunek między tym, jak mocno naciskasz, a tym, jak szybko idzie kanapa.
W rzeczywistości jest to bardzo podobne do obwodu elektrycznego prądu stałego, w którym przykłada się pewną ilość napięcia do obwodu, a prąd przepływa przez niego z odpowiednią szybkością.
W przypadku zarówno kanapy, jak i obwodu reakcja na Twój sygnał wejściowy może być prosta i dość liniowa: rezystor, który jest zgodny z prawem Ohma, gdzie jego impedancja elektryczna jest tylko rezystancją, a kanapa może mieć stopy suwaka tarcia, które pozwalają na to poruszać się z prędkością proporcjonalną do siły. *
Obwody i układy mechaniczne mogą być również nieliniowe. Jeśli obwód składa się ze zmiennego napięcia umieszczonego na rezystorze szeregowym z diodą, prąd będzie bliski zeru, dopóki nie przekroczysz napięcia przedniego diody, w którym to punkcie prąd zacznie przepływać przez rezystor, zgodnie z Ohmem prawo. Podobnie, kanapa siedząca na podłodze zwykle ma pewien stopień tarcia statycznego: nie zacznie się poruszać, dopóki nie naciska się z pewną siłą początkową. Ani w układzie mechanicznym, ani elektrycznym nie ma pojedynczej impedancji liniowej, którą można zdefiniować. Najlepiej jest raczej osobno zdefiniować impedancje w różnych warunkach. (Prawdziwy świat jest znacznie bardziej podobny do tego.)
Nawet gdy rzeczy są bardzo wyraźne i liniowe, należy zauważyć, że impedancja opisuje tylko stosunek - nie opisuje granic systemu i nie jest „zła”. Możesz zdecydowanie uzyskać tyle prądu / prędkości, ile chcesz (w idealnym systemie), dodając więcej napięcia / mocniej pchając.
Układy mechaniczne również dają całkiem dobre wyczucie impedancji prądu przemiennego. Wyobraź sobie, że jeździsz na rowerze. Z każdym pół-cyklem pedałów naciskasz w lewo, naciskasz w prawo. Możesz również wyobrazić sobie pedałowanie za pomocą jednej stopy i klipsa na palce, tak aby pchać i ciągnąć przy każdym cyklu pedału. Jest to bardzo podobne do przyłożenia napięcia prądu przemiennego do obwodu: popychasz i ciągniesz kolejno, cyklicznie, na określonej częstotliwości.
Jeśli częstotliwość jest wystarczająco wolna - na przykład gdy zatrzymujesz się na rowerze, problem z pchaniem pedałów jest po prostu problemem „dc”, jak pchanie kanapy. Kiedy jednak przyspieszysz, rzeczy mogą działać inaczej.
Załóżmy teraz, że jeździsz na rowerze z określoną prędkością, a twój rower ma trzy prędkości z niskim, średnim i wysokim przełożeniem. Średni wydaje się naturalny, hi-gear jest trudny do przyłożenia wystarczającej siły, aby zrobić różnicę, a na niskim biegu po prostu obracasz pedały, nie przenosząc żadnej energii na koła. Jest to kwestia dopasowania impedancji , w której można skutecznie przenosić moc na koła tylko wtedy, gdy wykazują one pewną fizyczną odporność na stopę - nie za dużo, nie za mało. Odpowiednie zjawisko elektryczne jest również bardzo powszechne; potrzebujesz linii o dopasowanej impedancji, aby skutecznie transmitować moc RF z punktu A do punktu B, a za każdym razem, gdy połączysz dwie linie transmisyjne razem, na interfejsie wystąpi pewna strata.
Opór, jaki pedały zapewniają stopom, jest proporcjonalny do siły nacisku, co jest ściśle związane z prostym oporem - szczególnie przy niskich prędkościach. Nawet w obwodach prądu przemiennego rezystor zachowuje się jak opornik (do pewnego momentu).
Jednak w przeciwieństwie do rezystora impedancja roweru zależy od częstotliwości. Załóżmy, że ustawiłeś rower na wysokim biegu, zaczynając od zatrzymania. Rozpoczęcie może być bardzo trudne. Ale kiedy już zaczniesz, impedancja prezentowana przez pedały spada wraz z przyspieszaniem, a gdy jedziesz bardzo szybko, może się okazać, że pedały mają zbyt małą impedancję, aby pochłonąć energię z twoich stóp. Tak więc w rzeczywistości istnieje impedancja zależna od częstotliwości ( reaktancja ), która zaczyna się na wysokim poziomie i obniża się w miarę zbliżania się do wyższej częstotliwości.
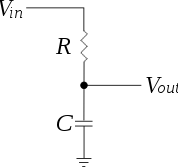
Jest to bardzo podobne do zachowania kondensatora, a dość dobrym modelem impedancji mechanicznej roweru byłby rezystor równolegle z kondensatorem.
Przy DC (zerowej prędkości) po prostu widzisz wysoką, stałą rezystancję jako impedancję. Wraz ze wzrostem częstotliwości pedałowania impedancja kondensatora staje się niższa niż rezystora i umożliwia przepływ prądu w ten sposób.
Istnieją oczywiście różne inne elementy elektryczne i ich analogie mechaniczne **, ale ta dyskusja powinna dać ci trochę wstępnej intuicji na temat ogólnej koncepcji pozostania uziemionym (zamierzona gra słów), gdy poznasz matematyczne aspekty tego, co czasami może się wydawać jak bardzo abstrakcyjny temat.
* Słowo dla wybrednych: prawo Ohma nigdy nie jest dokładne dla prawdziwego urządzenia, a siły tarcia w świecie rzeczywistym nigdy nie dają prędkości dokładnie proporcjonalnej do siły. Jednak „dość liniowy” jest łatwy. Staram się być tutaj edukatorem i tym podobne. Wytnij mi trochę luzu.
** Na przykład induktor jest czymś w rodzaju sprężynującego walca na kole, który zwiększa opór w miarę zwiększania częstotliwości)