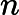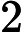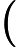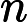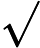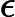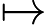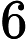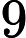Przykłady, w których wyjątkowość rozwiązania ułatwia znalezienie

37

Klasa złożoności składa się z tych -Problemy że może być określana przez wielomian czasu niedeterministycznych maszynie Turinga, który ma co najwyżej jedną ścieżkę akceptacji obliczeniowej. Oznacza to, że rozwiązanie, jeśli w ogóle, jest wyjątkowe w tym sensie. Uważa się wysoce nieprawdopodobne, że wszystkie -Problemy są , ponieważ przez Valiant-Vazirani twierdzenie to oznaczałoby upadek . $\mathsf{UP}$ $\mathsf{NP}$ $\mathsf{UP}$ $\mathsf{P}$ $\mathsf{NP}=\mathsf{RP}$

Z drugiej strony, nie ma -problem jest znany jako -Complete, co sugeruje, że unikalny wymóg rozwiązanie wciąż jakoś czyni je łatwiejszym. $\mathsf{UP}$ $\mathsf{NP}$

Szukam przykładów, w których założenie o wyjątkowości prowadzi do szybszego algorytmu.

Na przykład, patrząc na problemy z wykresem, czy maksymalna klika na wykresie może zostać znaleziona szybciej (choć być może wciąż w wykładniczym czasie), jeśli wiemy, że wykres ma unikalną maksymalną klikę? A może wyjątkowa kolorystyka, unikalna ścieżka hamiltonowska, unikalny minimalny zestaw dominujący itp.? $k$

Ogólnie rzecz biorąc, możemy zdefiniować wersję wyjątkowy roztwór o dowolnym -Complete problemu, skalowanie ich do . Czy wiadomo dla któregokolwiek z nich, że dodanie założenia o wyjątkowości prowadzi do szybszego algorytmu? (Pozwalając, że nadal jest wykładniczy). $\mathsf{NP}$ $\mathsf{UP}$

— Andras Farago
źródło

7

Twoje pierwsze zdanie zawiera poprawną definicję UP, ale resztą twoich odniesień do UP powinno być tak naprawdę PromiseUP (w tym Valiant-Vazirani). Tak czy inaczej jest to bardzo interesujące pytanie. Dwa przykłady: 1) Faktoring jest w UP i ma algorytm szybszy niż te znane z problemów z NP-zupełnym (ale faktoring jest również w coNP, a nawet coUP, więc nie jest tak jasne, że unikalność leży u podstaw szybkiego algorytmu.) 2 ) Sodoku, zgodnie z tradycyjną definicją, jest w PromiseUP, ale nie znam żadnych podejść do rozwiązywania sudoku, które wykorzystywałyby obiecaną wyjątkowość.

— Joshua Grochow

9

Parzystość liczby ścieżek hamiltonowskich można znaleźć w czasie

( arxiv.org/pdf/1301.7250.pdf ), podczas gdy najbardziej znany algorytm problemu decyzyjnego zajmuje prawie

czasu.

{1.618}^{n}

$1.618^n$

2^{n}

$2^n$

— Alex Golovnev

8

Oto przykład z obliczeń kwantowych: Rozważ problem wyszukiwania n elementów. Jeśli wiesz, że jest dokładnie 1 zaznaczony element, możesz go znaleźć za pomocą dokładnego algorytmu kwantowego z

zapytania. Jeśli nie znasz liczby zaznaczonych elementów, każdy dokładny algorytm kwantowy wymaga

zapytań.

Θ (\sqrt{n})

$\Theta(\sqrt{n})$

n

$n$

— Robin Kothari,

22

3-SAT może być jednym z takich problemów. Obecnie najlepsza górna granica dla Unique 3-SAT jest wykładniczo szybsza niż dla ogólnej 3-SAT. (Przyspieszenie jest wykładnicze, chociaż redukcja wykładnika jest niewielka.) Rekordzistą tego wyjątkowego przypadku jest ten artykuł autorstwa Timona Hertliego.

$k$ $k \geq 5$ $k$ $k$ $k = 3, 4$ $k$

$k$ $k$ $\delta < 1$ $n$ $k$ $O^*(2^{\delta n})$ $k \geq 3$ $k$ $k$ $k \geq 3, \epsilon > 0$ $k$ $O^*(2^{\epsilon n})$

$O^*$

— Andy Drucker
źródło

1

„prawda dla Unique 3-SAT”

\mapsto

$\: \mapsto \:$ „prawda dla Unique k-SAT”

$\;\;\;\;$

Cześć Ricky, nie widzę problemu z tym, co jest napisane. Ostatnie stwierdzenie o Unique 3-SAT znajduje się w streszczeniu artykułu.

— Andy Drucker,

k

$k$

$\hspace{1.58 in}$ co sprawiłoby, że byłoby to mylące.

$\;$

16

Najkrótszy problem ścieżki rozłącznej 2-wierzchołkowej na niekierowanych grafach ostatnio rozwiązany (ICALP14) przez A. Bjorklunda i T. Husfeldta. Ale rozwiązanie deterministyczne dotyczy przypadku rozwiązania unikalnego. W przypadku, gdy istnieje więcej niż jedno rozwiązanie, pokazali, że problem należy do RP . Jak wspomnieli autorzy artykułu, nie wiadomo, czy problem dotyczy P w ogólnym scenariuszu.

— Saeed
źródło

3

Dziękuję, to jest bardzo interesujące. Ogólny przypadek, w którym rozwiązanie nie jest unikalne, jest również dobrym przykładem naturalnego (lub nawet praktycznego) problemu graficznego, który obecnie okazuje się być w RP, ale nie jest znany w P.

— Andras Farago

10

Poza teorią złożoności i analizą algorytmów założenie, że może istnieć tylko jedno rozwiązanie, stanowi podstawę dla niektórych standardowych zasad używanych do dedukcji rozwiązania zagadek sudoku. Reguły te zazwyczaj obejmują poszukiwanie sposobów, w jakie części układanki mogą mieć dwa lub więcej rozwiązań, które nie wchodzą w interakcje z resztą układanki. Nie może się to zdarzyć w rzeczywistym rozwiązaniu, więc jeśli zostanie znaleziony wzorzec, który grozi jego spowodowaniem, należy go przerwać, umożliwiając solverowi ustalenie ograniczeń co do tego, jak może wyglądać rzeczywiste rozwiązanie. Zobacz http://www.brainbashers.com/sudokuuniquerectangles.asp kilka przykładów reguł dedukcji opartych na wyjątkowości.

— David Eppstein
źródło

9

$G$