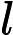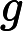Dlaczego wybór sortuje się szybciej niż sortowanie bąbelkowe?

Na Wikipedii napisano, że „... sortowanie selekcji prawie zawsze przewyższa sortowanie bąbelkowe i sortowanie gnomów”. Czy ktoś może mi wyjaśnić, dlaczego sortowanie jest uważane za szybsze niż sortowanie bąbelkowe, mimo że oba mają:

1. Złożoność najgorszego przypadku :$\mathcal O(n^2)$

2. Liczba porównań : $\mathcal O(n^2)$

3. Najlepsza złożoność czasu sprawy :

   • Sortowanie bąbelkowe:$\mathcal O(n)$
   • Wybór sortowania:$\mathcal O(n^2)$

4. Średnia złożoność czasu sprawy :

   • Sortowanie bąbelkowe:$\mathcal O(n^2)$
   • Wybór sortowania:$\mathcal O(n^2)$

Wszystkie podane przez Ciebie złożoności są prawdziwe, jednak podane są w notacji Big O , więc wszystkie wartości addytywne i stałe są pomijane.

Aby odpowiedzieć na twoje pytanie, musimy skoncentrować się na szczegółowej analizie tych dwóch algorytmów. Analizę tę można wykonać ręcznie lub znaleźć w wielu książkach. Wykorzystam wyniki z Knuth's Art of Computer Programming .

Średnia liczba porównań:

• Sortowanie bąbelkowe :$\frac{1}{2}(N^2-N\ln N -(\gamma+\ln2 -1)N) +\mathcal O(\sqrt N)$
• Sortowanie wstawek :$\frac{1}{4}(N^2-N) + N - H_N$
• Sortowanie wyboru :$(N+1)H_N - 2N$

Teraz, jeśli wykreślisz te funkcje, otrzymasz coś takiego:

Jak widać, sortowanie bąbelkowe jest znacznie gorsze wraz ze wzrostem liczby elementów, mimo że obie metody sortowania mają tę samą asymptotyczną złożoność.

Ta analiza opiera się na założeniu, że dane wejściowe są losowe - co może nie być prawdą przez cały czas. Jednak zanim zaczniemy sortowanie, możemy losowo permutować sekwencję wejściową (dowolną metodą), aby uzyskać średnią wielkość liter.

Pominąłem analizę złożoności czasu, ponieważ zależy to od implementacji, ale można zastosować podobne metody.

Koszt asymptotyczny, czyli matematyczna adnotacja , opisuje ograniczające zachowanie funkcji, ponieważ jej argument dąży do nieskończoności, tj. Jej tempa wzrostu.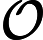$\mathcal O$

Sama funkcja, np. Liczba porównań i / lub swapów, może być inna dla dwóch algorytmów o tym samym koszcie asymptotycznym, pod warunkiem, że będą rosły z tą samą szybkością.

Mówiąc dokładniej, sortowanie bąbelkowe wymaga średnio zamian na wpis (każdy wpis jest przenoszony elementarnie z pozycji początkowej do końcowej, a każda zamiana obejmuje dwa wpisy), podczas gdy sortowanie selekcji wymaga tylko (raz minimalna / maksymalna została znaleziona, jest zamieniana raz na koniec tablicy).$n/4$$1$

Pod względem liczby porównań sortowanie bąbelkowe wymaga porównań , gdzie jest maksymalną odległością między pozycją początkową pozycji a jej pozycją końcową, która jest zwykle większa niż dla równomiernie rozłożonych wartości początkowych. Sortowanie selekcji wymaga jednak zawsze porównań .k n / 2 ( n - 1 ) × ( n - 2 ) /$k\times n$$k$$n/2$$(n-1)\times(n-2)/2$

Podsumowując, limit asymptotyczny daje dobre wyobrażenie o tym, jak rosną koszty algorytmu w stosunku do wielkości wejściowej, ale nie mówi nic o względnej wydajności różnych algorytmów w tym samym zestawie.

Sortowanie bąbelkowe wykorzystuje więcej czasów zamiany, podczas gdy sortowanie selekcyjne pozwala tego uniknąć.

Podczas korzystania z wyboru sortowania zamienia się nco najwyżej razy. ale przy użyciu sortowania bąbelkowego prawie zamienia się n*(n-1). Oczywiście czas czytania jest krótszy niż czas pisania, nawet w pamięci. Czas porównania i inny czas działania można zignorować. Czasy wymiany są więc kluczowym wąskim gardłem problemu.