Jelly to milczący , zorientowany na golfa język programowania autorstwa naszego własnego Dennisa . Coraz częściej pojawia się w odpowiedziach, pokonując inne języki golfa, takie jak Pyth i CJam, zarówno za pomocą własnej strony kodowej, jak i potężnego systemu łańcuchowego do zwięzłego wyrażania programów.

Zbierzmy przydatne wskazówki dotyczące gry w golfa w Galaretce. (Jak zawsze, jedna wskazówka na odpowiedź, proszę!)

Kompresja ciągów

Jeśli szukasz bardziej zoptymalizowanego / automatycznego kompresora strun, wypróbuj ten .

Wypróbuj online!

Wygląda na skompresowany ciąg znaków “...», w którym kropki są fragmentem danych zakodowanych w podstawie 250. Algorytm dekompresyjny jest nieco skomplikowany: fragment jest interpretowany jako liczba całkowita o „mieszanej podstawie”, z divmododłamywaniem różnych części tej liczby całkowitej i budowaniem z nich łańcucha.

Stworzyłem mały interfejs Python 3 do kompresji ciągów galaretki:

import dictionary
code_page = '''¡¢£¤¥¦©¬®µ½¿€ÆÇÐÑ×ØŒÞßæçðıȷñ÷øœþ !"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstuvwxyz{|}~¶°¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁼⁽⁾ƁƇƊƑƓƘⱮƝƤƬƲȤɓƈɗƒɠɦƙɱɲƥʠɼʂƭʋȥẠḄḌẸḤỊḲḶṂṆỌṚṢṬỤṾẈỴẒȦḂĊḊĖḞĠḢİĿṀṄȮṖṘṠṪẆẊẎŻạḅḍẹḥịḳḷṃṇọṛṣṭụṿẉỵẓȧḃċḋėḟġḣŀṁṅȯṗṙṡṫẇẋẏż«»‘’“”'''

class Compress(list):
    def character(self, c):
        if c in '\n\x7f¶':
            o = 95
        elif ' ' <= c <= '~':
            o = ord(c)-32
        else:
            raise ValueError(c + " is neither printable ASCII nor a linefeed.")
        self += [lambda z: 3*z+0, lambda z: 96*z+o]; return self
    def string(self, s):
        for c in s: self.character(c)
        return self
    def dictionary(self, w):
        ts = bool(self)
        if w[:1] == ' ': w = w[1:]; ts = not ts
        dct = dictionary.short if len(w) < 6 else dictionary.long
        W, sc = (w, 0) if w in dct else (w[:1].swapcase() + w[1:], 1)
        if W not in dct: raise ValueError(w + " isn't in the dictionary.")
        f = ts or sc; j = (2 if sc else 1) if ts else 0; i = dct.index(W)
        self += [lambda z: 3*z+2, lambda z: 3*z+j] if f else [lambda z: 3*z+1]
        self += [lambda z: 2*z+int(len(w) < 6), lambda z: len(dct)*z+i]
        return self
    def go(self):
        compressed = []; z = 0
        for f in self[::-1]: z = f(z)
        while z:
            c = z % 250
            if c == 0: c = 250
            z = (z - c) // 250
            compressed.append(code_page[c - 1])
        return '“{0}»'.format(''.join(compressed[::-1]))

Użyj kompresora w następujący sposób.

print(Compress()
      .dictionary('public')
      .dictionary(' static')
      .dictionary(' boolean')
      .string(' is')
      .dictionary('Power')
      .string('Of')
      .dictionary('Ten')
      .string('(')
      .dictionary('long')
      .dictionary(' input')
      .string(') {\n ')
      .dictionary(' return')
      .string('\n   ')
      .dictionary(' input')
      .string(' ==')
      .go())

Compress jest konstruktorem ciągów:

• .string(s) wstawi nieprzetworzone, drukowalne znaki ASCII do łańcucha.

  (Każdy znak kosztuje około 0,827 skompresowanych bajtów).

• .dictionary(w)wyszukuje ciąg znaków we wbudowanych słownikach Jelly. Możesz rozpocząć ciąg od pojedynczej spacji, jeśli chcesz. Jeśli będzie to musiało odbiegać od normalnego zachowania polegającego na dodawaniu ciągów znaków lub odwracać wielkie litery w słowniku, odpowiednio doda flagi.

  (Kosztuje około 1,997 bajtów w przypadku krótkich słów, 2,433 bajtów w przypadku długich słów; jeśli są flagi, dodaj 0.199 bajtów.)

Jest to część tego, co stało się tutorialem Jelly wiki .

Więzy

(Jest to swego rodzaju kontynuacja programowania ukrytego .)

Jak Jelly ocenia łańcuch? Jak wyjaśniono wcześniej, należy wziąć pod uwagę trzy przypadki: czy łańcuch ten nazwano niladycznie , monadycznie , czy dyadycznie .

1. Łańcuchy niladowe

Są to najłatwiejsze z tej grupy. Aby ocenić łańcuch niladowy rozpoczynający się od nilada, na przykład α f g h, oceń łańcuch monadyczny f g hna tym niladzie α. (Zastrzeżenia: jeśli cały łańcuch jest pusty, zamiast tego zwracane jest 0. Jeśli α nie jest to nilad, α=0zamiast tego użyj use .)

Na przykład 4½jest po prostu ½oceniane na 4, co jest 2.

2. Łańcuchy monadyczne

Łańcuchy monadyczne są rozkładane od lewej do prawej, dopóki nie pozostaną żadne linki do rozważenia. Przekazano nam również trochę argumentów ω. Na dwa pytania należy odpowiedzieć:

Jaka jest początkowa wartość tej oceny od lewej do prawej?

• Jeśli nasz łańcuch zaczyna się od nilada α, a po nim następuje zero lub więcej monad (jak ½), pary dyad-nilad (jak +2) i pary nilad-dyad (jak 4*): zaczynamy od oceny α, a następnie rozważamy resztę łańcucha .

• W przeciwnym razie zaczniemy od argumentu przekazanego do tego łańcucha ωi rozważymy cały łańcuch.

Jak schodzimy z łańcucha?

Nazwijmy Vbieżącą wartość - początkowo jest to wartość opisana powyżej, ale dostaje aktualizację w miarę przechodzenia przez łańcuch - i oznacza

• nilady za pomocą cyfr,
• monady używające małych liter,
• dyads wykorzystaniem symboli operatora +, ×, ÷.

Następnie dopasowywane są następujące wzory, od góry do dołu:

                                 ┌───────────┬─────────┐
                                 │ old chain │ new V   │
                                 ╞═══════════╪═════════╡
                                 │ + × 1 ... │ (V+ω)×1 │ *
                                 │ + f ...   │ V+f(ω)  │
                                 │ + 1 ...   │ V+1     │
                                 │ 1 + ...   │ 1+V     │
                                 │ + ...     │ V+ω     │
                                 │ f ...     │ f(V)    │
                                 └───────────┴─────────┘
      (* Only if `...` consists of monads, dyad-nilad pairs, and nilad-dyad pairs.)

Wypróbujmy to na łańcuchu +²×.

• +nie jest niladem, więc zaczynamy od V = ω.
• Następnie odcinamy +², dopasowując drugi wzór i otrzymujemy V = ω+ω².
• Następnie odcinamy ×, dopasowując piąty wzór i otrzymujemy V = (ω+ω²)×ω.
• Łańcuch jest teraz pusty, podobnie jak (ω+ω²)×ωnasz końcowy wynik.

3. Łańcuchy dyadyczne

Są to w zasadzie łańcuchy monadyczne, ale tym razem istnieją dwa argumenty: λ(lewy) i ρ(prawy).

Jaka jest wartość początkowa?

• Jeśli łańcuch zaczyna się od trzech podobnych diad + × %, zaczynamy od λ+ρi rozważmy łańcuch × % ...dalej.

• W przeciwnym razie zaczniemy od λi rozważymy cały łańcuch.

Jak schodzimy z łańcucha?

Tym razem wzory są

                                 ┌───────────┬─────────┐
                                 │ old chain │ new V   │
                                 ╞═══════════╪═════════╡
                                 │ + × 1 ... │ (V+ρ)×1 │ *
                                 │ + × ...   │ V+(λ×ρ) │
                                 │ + 1 ...   │ V+1     │
                                 │ 1 + ...   │ 1+V     │
                                 │ + ...     │ V+ρ     │
                                 │ f ...     │ f(V)    │
                                 └───────────┴─────────┘
      (* Only if `...` consists of monads, dyad-nilad pairs, and nilad-dyad pairs.)

Wypróbujmy to na łańcuchu +×÷½.

• Łańcuch zaczyna się od trzech diad, więc zaczynamy od V = λ+ρi wyrzucamy +.
• Następnie odcinamy ×÷, dopasowując drugi wzór i otrzymujemy V = (λ+ρ)×(λ÷ρ).
• Następnie odcinamy ½, dopasowując szósty wzór i otrzymujemy V = sqrt((λ+ρ)×(λ÷ρ)).
• Łańcuch jest teraz pusty, więc skończyliśmy.

Wartości liczbowe w specjalnych przypadkach

Oto kilka specjalnych przypadków dla parsera liczbowego Jelly:

• - ocenia na -1
• . ocenia na 0.5
• ȷocenia na 1000( ȷsłuży do zapisu naukowego, np. 2ȷ6jest 2000000)
• ıewaluuje do 1j( ıjest dla liczb zespolonych, np. 2ı3jest 2+3j)

Warto również zauważyć, że coś takiego 4ıjest w rzeczywistości 4+1j, a nie 4.

Możesz je mieszać i dopasowywać, np .:

• -.jest -0.5i -ȷjest-1000
• -ıjest -1+1j, ı-jest -1ji -ı-jest-1-1j
• .ȷ jest 500.0
• .ıjest 0.5+1j, ı.jest 0.5ji .ı.jest0.5+0.5j
• ȷıjest 1000+1j, ıȷjest 1000ji ȷıȷjest1000+1000j

Zauważ, że ȷ-tak 0.1, ale to nie oszczędza żadnych bajtów .1. Są też następujące rzeczy, które można już wykonać w odpowiedniej liczbie bajtów za pomocą wbudowanej zmiennej dla 10 ( ⁵), ale mogą być przydatne w rzadkim przypadku, gdy wbudowane jest niedostępne lub oszczędzić na konieczności używania ¤:

• ȷ.jest sqrt(10) ~ 3.162277, .ȷ.jest sqrt(10)/2 ~ 1.5811i ȷ-.jest1/sqrt(10) ~ 0.31162

Zoptymalizowany kompresor strunowy

Wypróbuj online!

Post Lynn szczegółowo opisuje, czym dokładnie są skompresowane ciągi, wraz z posiadaniem kompresora, który wytworzy te skompresowane ciągi. Jednakże, podczas gdy majstrować wokół z programu w galarecie, znalazłem to męczące musiał połączyć .dictionaryi .stringwraz z poprawnymi docelowych pomieszczeń i tak dalej, i tak dalej, w celu osiągnięcia możliwie najkrótszy łańcuch.

Dlatego postanowiłem utworzyć rozszerzenie skryptu Lynn, które pobierałoby dane od użytkowników i znajdowało najkrótszy sposób, aby można go było skompresować bez konieczności wykonywania jakiejkolwiek pracy. Skrypt jest dość długi, dlatego dodałem łącze TIO, a nie sam kod.

Sposób działania programu polega na kompresji za pomocą 3 różnych metod i określeniu, który jest najkrótszy:

1. Metoda 1 po prostu koduje każdy bajt wejścia na raz, co zwykle daje najdłuższy wynik w porównaniu z innymi. Nawet gdy dane wejściowe są bardzo krótkie, nadal udaje im się stworzyć dość długie alternatywy. Na przykład najkrótsza droga, którą testmożna skompresować “¡ḌY», to metoda ta zwraca “¡⁷ƑKʂ»(2 bajty dłużej). Zasadniczo działa to tylko wtedy, gdy łańcuch ma mniej niż 4 znaki

2. Druga metoda dzieli ciąg na słowa i znaki interpunkcyjne, ponieważ są one dodawane do kompresora na różne sposoby. Słowa, które są częścią słownika, są dodawane za pomocą .dictionarymetody kodu Lynn, która kompresuje je bardziej, niż gdyby były dodawane po prostu przez punkty kodowe. Jednak interpunkcja musi być dodana przez punkt kodowy, ponieważ niestety nie są one częścią słownika.

   Interpunkcja obejmuje spacje, w których wchodzi metoda numer 3, ale najpierw i ocena metody 2: porównajmy metodę pierwszą i drugą kompresującą ciąg znaków Hello, World!(zawiera słowa, interpunkcję i spacje, więc jest idealna). Kompresja znak po znaku powoduje końcowy ciąg “ŒCdẉa÷¹ṂȤƓ(Ẋ)»(15 bajtów), który, jak się okazuje, jest dłuższy niż łatwiejszy sposób na wyjście Hello, World !: “Hello, World!. Teraz spójrzmy na metodę drugą. Daje to skompresowany ciąg znaków, “Ọƥ⁷Ƭė3⁶»który waży 9 bajtów, co stanowi wielką poprawę w stosunku do starego. Jednak najkrótsze Witaj, świecie! program w galarecie ma 8 bajtów , więc coś można poprawić

3. Oto metoda 3, dzięki której jest jeszcze krótsza. Zgodnie z oczekiwaniami wyjście dla Hello, World jest oczywiście “3ḅaė;œ»najkrótszym możliwym programem. Co robi metoda 3, a metoda 2 nie? Metoda 3 łączy pojedyncze przestrzenie w wiodące, dla których dekompresor Jelly ma flagę. W kodzie zarówno dla kompresora, jak i dekompresora można zobaczyć kod podobny if flag_space: word = ' ' + word, pokazujący, że spacje wiodące są a) obsługiwane i b) oszczędzania bajtów. Dlatego rozdzielacz ciągów z metody drugiej jest dostosowywany tak, że same spacje są łączone w ciąg bezpośrednio po nim, aby utworzyć ciągi wiodące. Oznacza to, że Hello, World!jest analizowany jako ["Hello", ",", " World", "!"], który po skompresowaniu ma tylko 6 bajtów (8, jeśli zawiera separatory). Jest to prawie zawsze najkrótsza metoda kompresji, z wyjątkiem dodanego „rozszerzenia”,

Jest to większość programu, ale jest jeszcze kilka opcji, które pomagają jeszcze bardziej kompresować dane.

• Program sprawdza, czy każda skompresowana wersja jest poprawna, za pomocą dekompresora ss Dennisa używanego przez Jelly (przejdź bezpośrednio do źródła)
• Możesz zobaczyć wszystkie różne skompresowane ciągi, tworząc pierwszy argument wiersza poleceń --debug, który zamiast po prostu pokazywać najkrótszy skompresowany ciąg, pokazuje wszystkie 3 wraz z kopią „To jest najkrótszy”
• Program obsługuje „nie-słowa”

Bez słów

Rozpocząłem pracę nad kompresorem Lynna po tym , jak zobaczyłem ten komunikat, zrobiłem sobie z niego frustrację i denerwowałem się tym, że nie mogłem znaleźć najkrótszego sposobu na skompresowanie go (to 29 lub 32 bajty dla rekordu). Jednak podczas testowania moich ulepszeń odkryłem, że takich słów knownsnie ma w słowniku Jelly. Dlatego postanowiłem znaleźć sposób na skompresowanie tych „nie-słów” w najkrótszym możliwym kodzie Jelly.

Utworzyłem funkcję ( trim), która dzieli ciąg jako punkt, w którym co najmniej jedna z jego części to słowa. Na przykład knownszostałby podzielony na, ["known", "s"]a program dodałby pierwsze słowo za pomocą słownika add ( .dictionary), a drugą część słowa za pomocą .stringwywołania. Ale to wciąż pozostawia dwa przypadki krawędzi: ciągi, które nie zawierają w sobie słów (takich jak ajdl) i nie-słowa, które mają słowa na końcu, takie jak abctest, które nie zostałyby podzielone przez trimfunkcję.

Ponieważ nie ma sposobu na znalezienie słów w ciągu, w którym nie ma słów, najprostszym i najkrótszym sposobem ich obsługi jest dodanie ich znak po znaku za pomocą .stringwywołania. Zostanie ajdldodany przez .string('ajdl'). Natomiast słowa, które kończą się rozpoznanymi słowami, zasadniczo trymują, ale odwrotnie, i nakładają .dictionaryi .stringodwrotnie do trymera do przodu.

Jak się okazuje, przycinanie łańcucha, zarówno od początku, jak i od końca, jest oczywiście krótsze niż dodawanie każdego znaku do kompresora, jak pokazano na wejściu abctest this string, co daje wynik debugowania

Original        : abctest this string

Optimised       : “¡J+v(p⁸ụƘ$,»
Seperate spaces : “Ç⁴ṭḍµḄ7oeṂdḷp»
No trimmer      : “¤ɦ?Ɓ¢#fḲOạ⁾¶ɼȥƬ»
All characters  : “µẓþ"Y7_ḣṗḢ))9Þ⁴⁺Ẉ²)ɱ»
Non-compressed  : “abctest this string
Shortest        : “¡J+v(p⁸ụƘ$,»
=====

Różnica między optymalną mocą wyjściową (która używa trymera) a tą, która tego nie robi, to aż 4 duże bajty. Wreszcie, zdarzają się sytuacje, w których sam łańcuch jest krótszy niż jakakolwiek skompresowana wersja, w której teraz uwzględniono.

Oczywiście wiele zasług to Lynn za stworzenie oryginalnej sprężarki

Możesz użyć indeksu górnego trzy do dziewięciu ( ³⁴⁵⁶⁷⁸⁹), aby zagrać w niektóre używane wartości, ale zależy to od liczby argumentów wiersza poleceń, aw przypadku linków - od argumentów linków.

• ³ zwraca 100 i działa tylko wtedy, gdy nie ma danych wejściowych.
• ⁴ zwraca 16 i działa tylko, jeśli istnieje co najwyżej jedno wejście.
• ⁵ zwraca 10 i działa tylko wtedy, gdy są najwyżej dwa wejścia.
• ⁶ zwraca spację, jeśli są co najwyżej trzy wejścia.
• ⁷ zwraca nowy wiersz, jeśli są maksymalnie cztery wejścia.

Jeśli masz pięć wejść, nie masz szczęścia.

Niedawno nowa wersja języka obniżyła wartość ³do 100 i wprowadziła nowe atomy, które zwracają wartości lub (dla linków) ich argumenty.

• ⁸ zwraca pustą listę wszędzie oprócz łączy, do których przekazano lewy argument.
• ⁹ zwraca 256 wszędzie, z wyjątkiem łączy, do których przekazano odpowiedni argument.

Jeśli masz link i masz do niego argumenty z obu stron, nie masz szczęścia.

Błędy w nadużyciach

Podziękowania należą się Adnanowi za skorzystanie z tego pierwszego w Napisz program do uelastycznienia łańcuchów .

Galaretka ma pewnego dnia uzyskać arytmetykę postaci, ale dopóki tak się nie stanie, możemy skorzystać z faktu, że Python przeciąża większość operatorów arytmetycznych i że Jelly nie sprawdza typu.

Na przykład

“abcd”Ḥ

nie powinien teraz robić nic przydatnego, ale ponieważ Ḥ(unhalve) jest zaimplementowane jako

lambda z: z * 2

i atomy arytmetyczne wektoryzują na głębokości 0 (tzn. działają na liczbach lub znakach), powyższy kod Jelly daje

['aa', 'bb', 'cc', 'dd']

Uważaj, aby to tworzyło rzeczywiste ciągi w języku Python (typ galaretki nie powinien mieć), więc nie będzie to przydatne we wszystkich sytuacjach.

Podobnie, +/może być użyteczne do łączenia łańcuchów, z tymi samymi zastrzeżeniami.

Optymalny kompresor strunowy

Niedawno zapytałem Erika Outgolfera o dodanie zoptymalizowanego kompresora łańcuchów do strony referencji JHT , ale powiedzieli, że

przepraszam, ale ten kompresor nie wydaje się być w pełni wdrożony
, mówi, że “ugtestslug”jest najkrótszy z możliwych ugtestslug, jednocześnie “#ṀȮụḄPƇ»wykonując zadanie

Postanowiłem więc wdrożyć optymalną sprężarkę strunową.

Proste podejście, ale gwarantuje znalezienie najmniejszej możliwej wartości (a tym samym liczby bajtów)

Weź dane wejściowe stdin, dane wyjściowe do stdout. Podobnie jak oryginalny kompresor, ¶lub (dosłowny znak nowej linii) można wprowadzić jako nową linię.

Próba uruchomienia go z dużą ilością znaków interpunkcyjnych (na przykład danych wejściowych ¶-----¶) spowoduje wyświetlenie nieskompresowanego ciągu.

Oczywiście wiele zasług to Lynn za stworzenie oryginalnej sprężarki .

Jest to część tego, co stało się tutorialem Jelly wiki .

Programowanie ukryte

Galaretka jest milczącym językiem programowania. Oznacza to, że definiujesz linki (funkcje) poprzez komponowanie istniejących linków w łańcuch , bez wyraźnego mówienia o zaangażowanych argumentach. Sposób, w jaki argumenty „przepływają” przez tę kompozycję, jest określony przez wzorzec, w którym ułożone są linki. Przykład tego zostanie podany wkrótce, ale najpierw musimy wprowadzić kilka pojęć.

Arity łącza jest bardzo istotne pojęcia. Wszystkie atomy - wbudowane, podobne +i ½- mają ustalone arie. Linki są podzielone na trzy kategorie, w zależności od ich pochodzenia:

• Nilady nie przyjmują argumentów (arity 0); inne niż niektóre polecenia I / O i stanowe, w większości reprezentują stałe wartości. Na przykład dosłowność3 to nilad.

• Monady biorą jeden argument (arity 1). (Nie ma tutaj połączenia z funkcjonalnymi programami monad.) Na przykład ½(pierwiastek kwadratowy) jest monadą.

• Diady biorą dwa argumenty (arity 2): lewy i prawy. Na przykład +jest diadem.

(Używając przymiotników, mówimy, że link jest niladyczny , monadyczny lub dyadyczny ).

Więc jaki jest sens linków, które definiujemy podczas pisania programu? Domyślnie są one różne - to znaczy od dzwoniącego zależy, ile argumentów użyć, a w przypadku zależy, ile argumentów głównego łącza zależy to od liczby argumentów przekazanych przez program.

Na przykład +½jest łańcuchem +(dodawania) i ½(pierwiastka kwadratowego). Ponieważ odpowiednie aromaty elementów tego łańcucha to 2 i 1, nazywamy go łańcuchem 2,1 . Interpretator ma określone zasady rozkładania łańcuchów, w zależności od ich arsenałów: reguły te dyktują, że biorąc pod uwagę dane wejściowe n, ten nowy link oblicza n + sqrt(n). (Możesz odczytać +½jako „... plus pierwiastek kwadratowy”. )

Zatem programowanie w stylu galaretki jest w zasadzie sztuką dobrego uczenia się tych zasad i tworzenia sprytnych łańcuchów, które wykonują zadanie, milcząco .

Jest to część tego, co stało się tutorialem Jelly wiki .

Struktura programu

Każda linia w programie Jelly jest definicją łącza . Linki są w zasadzie funkcjami. Dolna linia reprezentuje „ main”: to link jest oceniany za pomocą argumentów przekazanych w wierszu poleceń.

Wszystkie linki oprócz ostatniego są zatem definicjami funkcji: możesz się do nich odwoływać za pomocą aktorów . Na przykład çjest „linkiem powyżej tego, jako operatora binarnego (diada)” . Rozważ ten przykładowy program , który oblicza kwadrat sumy swoich argumentów:

+
ç²

To jest trochę jak pseudokod:

define f:
    the built-in link +
define main:
    apply the dyad f
    square the result

Jest to część tego, co stało się tutorialem Jelly wiki .

Łącza wielołańcuchowe

Pamiętasz, jak napisałem, że definiujesz link, tworząc łańcuch innych linków? Nie mówiłem całej prawdy: w rzeczywistości jest to proces dwuwarstwowy. Łącze to łańcuch łańcuchów i domyślnie łańcuch zewnętrzny ma po prostu długość jednostkową.

Rozważ ten program:

C+H

To uzupełnienie plus połowa . Pobiera wartość wejściową ni oblicza (1-n)+(n/2). Nie zbyt ekscytujące, wiem. Ale struktura jest naprawdę taka:

Link, który napisaliśmy, jest w rzeczywistości łańcuchem zawierającym pojedynczy łańcuch.

Załóżmy, że (1-n)+(1-n)(n/2)zamiast tego chcemy obliczyć . Łańcuch dynamiczny +×działałby: według reguł łączenia oblicza λ+(λ×ρ), co wygląda bardzo podobnie do tego, czego potrzebujemy. Jednak zwykłe zastąpienie +przez +×w naszym programie nie zadziała: C+×Hjest to 1,2,2,1-łańcuchowy - uzupełnienie, następnie dodanie (argument), a następnie pomnożenie przez połowę - obliczenia((1-n)+n)×(n/2) .

Chcemy, aby Galaretka traktowała +×jako jednostkę i tworzyła łańcuch 1,2,1 z podłańcuchów C,+× oraz H. Łącza wielołańcuchowe pozwalają nam to zrobić! Aby je skonstruować, używamy separatorów łańcucha øµð : na powyższym obrazku wprowadziliby nowy niebieski prostokąt, odpowiednio o arity 0, 1 i 2. W naszym przypadku możemy pogrupować łańcuchy tak, jak chcemy, pisząc Cð+×µH:

Nie ma sposobu, aby zagnieździć te rzeczy jeszcze bardziej. Zamiast tego musisz zdefiniować wiele łączy.

Jeśli TMTOWTDI, wybierz ten, który pasuje do twojego łańcucha.

Jedną z zalet milczącego języka jest to, że zwykle można uciec bez używania zmiennych odniesień. Działa to jednak tylko wtedy, gdy linki w twoim łańcuchu mają odpowiednie aranżacje.

Na przykład prosty sposób pobrania sumy wszystkich tablic w tablicy 2D to

S€

który mapuje atom sumy na wszystkie elementy tablicy.

Teraz powiedz, że masz monadyczny łańcuch składający się z atomu

*

który mapuje każdy x tablicy 2D na x ^x . Na przykład dla A = [[1, 2], [3, 1], [2, 3]] wywołanie łańcucha dałoby [[1, 4], [27, 1], [4, 27]] .

Teraz chcemy wziąć sumę każdej pary. Niestety,

*S€

nie działa, ponieważ *nie działa już jak hak (użycie samego A jako poprawnego argumentu), ale jako rozwidlenie , co oznacza, że najpierw S€stosuje się do A , a wynikiem jest poprawny argument* .

Naprawienie tego jest dość łatwe:

*¹S€
*⁸S€

Oba dają pożądany wynik: *¹jest rozwidleniem, w którym ¹znajduje się funkcja tożsamości, i *⁸jest na szczycie , gdzie ⁸jest odwołanie do lewego argumentu łańcucha ( A ).

Istnieje jednak sposób na zaoszczędzenie bajtu! Atop ḅ1(konwertuj z unarnego na całkowity) również oblicza sumę każdej tablicy w A ^A , ale w przeciwieństwie do S€, ḅjest diademem łącza.

Łańcuch

*ḅ1

zwraca [5, 28, 31] (zgodnie z życzeniem); ponieważ ḅjest dyadyczny, *haczyki zamiast rozwidlenia

Kompresja liczb całkowitych

Kompresja ciągów jest przydatna podczas tworzenia tekstu w języku angielskim, ale jeśli potrzebujesz kompresować dane innego rodzaju, jest to dość nieskuteczne. W związku z tym przez większość czasu chcesz przechowywać dużą stałą w swoim programie, najlepiej przechowywać ją jako liczbę całkowitą.

Teraz, gdy Jelly ma swoją własną stronę kodową jako stałą, algorytm kompresji liczb całkowitych jest najprościej wyrażony w samej Galaretce:

ḃ250ịØJ”“;;”’ṄV

Wypróbuj online!

(Powyższy program zawiera również zaznaczenie pokazujące wartość, którą dekompresuje liczba całkowita.)

Oprócz zwykłego użycia liczby całkowitej jako liczby całkowitej, możesz także użyć go do utworzenia ciągu poprzez wykonanie na nim konwersji bazowej, a następnie indeksowanie w alfabet znaków. ṃAtom zautomatyzować ten proces, i jest dość użyteczny, ponieważ może to opisują cały proces rozprężania (inne niż alfabetu są dekompresowane w) w jednym bajcie.

Użyj produktów zewnętrznych, aby utworzyć przydatne macierze liczb całkowitych

Oto lista, którą stworzyłem w tym poście z nieco ładniejszym formatowaniem tabeli HTML.

Produkt zewnętrzny þmożna szybko przymocować do diada i powoduje, że diada działa na każdą parę elementów w swoich argumentach po lewej i prawej stronie. To jest skrót od €Ð€. Na przykład, gdybyśmy mieli kod [1,2]+€Ð€[0,10], moglibyśmy go skrócić [1,2]+þ[0,10] i obaj by się poddali [[1,2],[11,12]]. Odniosę się do diada z þzastosowanym (np+þ ) Jako diady produktu zewnętrznego.

Gdy liczba całkowita jest jednym z argumentów diady produktu zewnętrznego, Jelly najpierw przyjmuje zakres tej liczby, a następnie wykorzystuje wynik jako argument. Wiedząc o tym, powyższy przykład można dodatkowo skrócić2+þ[0,10] . Dotyczy to zarówno lewego, jak i prawego argumentu zewnętrznej diady produktowej.

Niektóre diady produktu zewnętrznego, gdy działają monadycznie na liczbę całkowitą, dają pewne matryce liczb całkowitych, które mogą być przydatne w grze w golfa (zwłaszcza wyzwania w sztuce ASCII), ale skonstruowanie ich zajęłoby wiele bajtów. Na przykład =þpo zastosowaniu do liczby całkowitej ndaje n×nmacierz tożsamości. Wypróbuj =þonline!

Poniżej znajduje się tabela diad i rodzaj matryc, które dają, gdy zamieniane są w diady produktu zewnętrznego i działają monadycznie na liczbę całkowitą. Diady wymienione w tym samym rzędzie dają te same matryce. Istnieje dyads nie zostały uwzględnione w tabeli jak &, |, %, w, ẇi ḍże również produkować całkowitą macierzy, ale ich wzory nie są tak proste i będzie prawdopodobnie mniej przydatny w sytuacjach. Wypróbuj wþonline!

+ ------------------------------------------------- ---- +
| Dyad | Wynikowa macierz | Przykład |
+ ------------------------------------------------- ---- +
| = ⁼ | | 1 0 0 |
| ċ | Macierz tożsamości | 0 1 0 |
| | | 0 0 1 |
+ ------------------------------------------------- ---- +
| | Elementy powyżej przekątnej wynoszą 1, | 0 1 1 |
| <| wszystkie pozostałe elementy mają wartość 0 | 0 0 1 |
| | | 0 0 0 |
+ ------------------------------------------------- ---- +
| | Elementy poniżej przekątnej wynoszą 1, | 0 0 0 |
| > | wszystkie pozostałe elementy mają wartość 0 | 1 0 0 |
| | | 1 1 0 |
+ ------------------------------------------------- ---- +
| | Elementy ukośne to 0, | 0 1 1 |
| n ⁻ | elementy ukośne są 1 | 1 0 1 |
| | | 1 1 0 |
+ ------------------------------------------------- ---- +
| a ȧ | | 1 1 1 |
| ṛ ị | Indeks wierszy każdego elementu | 2 2 2 |
| | | 3 3 3 |
+ ------------------------------------------------- ---- +
| o ḷ | | 1 2 3 |
| ȯ | Indeks kolumnowy każdego elementu | 1 2 3 |
| | | 1 2 3 |
+ ------------------------------------------------- ---- +
| | Główna przekątna wynosi 0, górna | 0 1 2 |
| _ | przekątne wynoszą 1, 2 ..., niższe | -1 0 1 |
| | przekątne wynoszą -1, -2 ... | -2 -1 0 |
+ ------------------------------------------------- ---- +
| | Główna przekątna wynosi 0, niższa | 0 -1 -2 |
| _ @ | przekątne wynoszą 1, 2 ..., górne | 1 0–1 |
| | przekątne wynoszą -1, -2 ... | 2 1 0 |
+ ------------------------------------------------- ---- +
| | Główna przekątna wynosi 0, górna | 0 1 2 |
| ạ | a dolne przekątne wynoszą 1, | 1 0 1 |
| | 2, 3 ... | 2 1 0 |
+ ------------------------------------------------- ---- +
| | | 2 3 4 |
| + | Indeks wiersza plus indeks kolumny | 3 4 5 |
| | | 4 5 6 |
+ ------------------------------------------------- ---- +
| | Minimum rzędu | 1 1 1 |
| «| i indeksy kolumnowe 1 2 2 |
| | | 1 2 3 |
+ ------------------------------------------------- ---- +
| | Maksymalna liczba rzędów | 1 2 3 |
| »| i indeksy kolumnowe 2 2 3 |
| | | 3 3 3 |
+ ------------------------------------------------- ---- +

Lista poleceń i literałów

Jeśli spróbujesz użyć wielu poleceń listy bez wektoryzacji na literale n lub liście literałów z , polecenie listy najpierw skonwertuje się na jakąś listę, a następnie wykona polecenie na tej liście.

Te polecenia pojawiają się przy użyciu wywołań iterablefunkcji w jelly.py .

def iterable(argument, make_copy = False, make_digits = False, make_range = False):
    the_type = type(argument)
    if the_type == list:
        return copy.deepcopy(argument) if make_copy else argument
    if the_type != str and make_digits:
        return to_base(argument, 10)
    if the_type != str and make_range:
        return list(range(1, int(argument) + 1))
    return [argument]

Oto kilka niekompletnych list tego, co zrobią te polecenia listy.

Zawija się w listę

Najprostszy powrót z iterable aby zawinąć argument na listę i zwrócić ten, który ma zostać przetworzony przez funkcję. Dzieje się tak, jeśli argument nie jest już listą, jest łańcuchem, a iterableargumenty nie wymagają innych metod.

-------------------------------------------------------------------------------
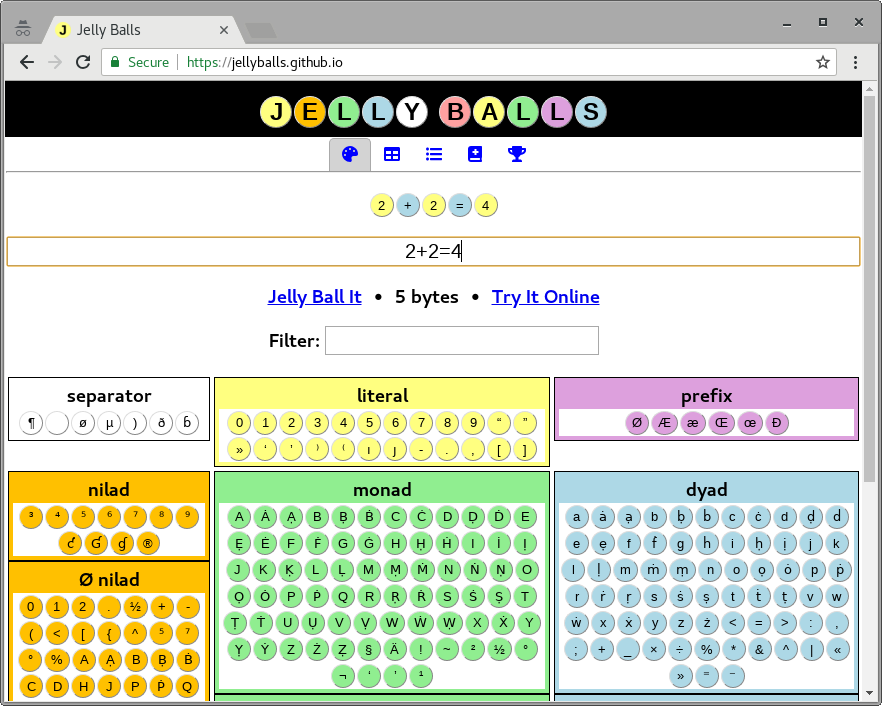
| Command | Description     | Process                       | Effect          |
-------------------------------------------------------------------------------
| F       | Flattens a list | 4953F -> [4953]F -> [4953]    | Same as W       |
-------------------------------------------------------------------------------
| G       | Format a list   | 4953G -> [4953]G -> [4953]    | Same as W       |
|         | as a grid       |                               |                 |
-------------------------------------------------------------------------------
| I       | Increments      | 4953I -> [4953]I -> <nothing> | Empty list      |
-------------------------------------------------------------------------------
| S       | Sums a list     | 4953S -> [4953]S -> 4953      | Same as ¹       |
-------------------------------------------------------------------------------
| Ṭ       | Boolean array,  | 4Ṭ -> [4]Ṭ -> [0, 0, 0, 1]    | n-1 zeroes,     |
|         | 1s at indices   |                               | 1 at end        |
-------------------------------------------------------------------------------
| Ụ       | Sort indices by | 4Ụ -> [4]Ụ -> [1]             | Yields [1]      |
|         | by their values |                               |                 |
-------------------------------------------------------------------------------
| Ė       | Enumerate list  | 4Ė -> [4]Ė -> [[1, 4]]        | Yields [[1, n]] |
-------------------------------------------------------------------------------
| Ġ       | Group indices   | 4Ġ -> [4]Ġ -> [[1]]           | Yields [[1]]    |
|         | by values       |                               |                 |
-------------------------------------------------------------------------------
| Œr      | Run-length      | 4Œr -> [4]Œr -> [[4, 1]]      | Yields [[n, 1]] |
|         | encode a list   |                               |                 |
-------------------------------------------------------------------------------

Konwertuj na bazę 10

Funkcje tutaj wywołują iterablekonwersję na liczbę na listę jej cyfrD , a następnie uruchamiają te cyfry.

-------------------------------------------------------------------------
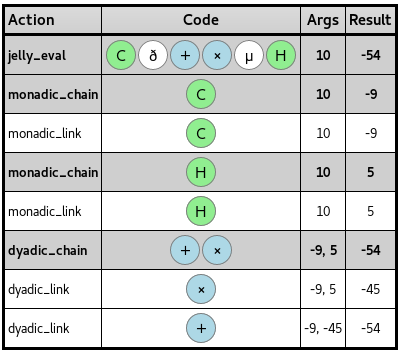
| Command | Description     | Process                      | Effect     |
-------------------------------------------------------------------------
| Q       | Unique elements | 299Q -> [2, 9, 9]Q -> [2, 9] | Unique     |
|         | ordered by      |                              | digits     |
|         | appearance      |                              | of n       |
-------------------------------------------------------------------------
| Ṛ       | Non-vectorized  | 4953Ṣ -> [4, 9, 5, 3]Ṛ       | Reverses D |
|         | reverse         | -> [3, 5, 4, 9]              |            |
-------------------------------------------------------------------------
| Ṣ       | Sort a list     | 4953Ṣ -> [4, 9, 5, 3]Ṣ       | Sorts D    |
|         |                 | -> [3, 4, 5, 9]              |            |
-------------------------------------------------------------------------

Konwertuj na listę z zakresem

Funkcje tutaj konwertują liczbę na zakres R = [1 ... n], a następnie działają w tym zakresie.

-----------------------------------------------------------------------------------------
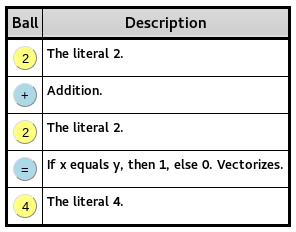
| Command | Description       | Process                             | Effect            |
-----------------------------------------------------------------------------------------
| X       | Random element    | 4R -> [1 ... 4]X -> 2               | Random element    |
|         |                   |                                     |  of R             |
|         |                   |                                     |                   |
-----------------------------------------------------------------------------------------
| Ḋ       | Dequeue from list | 4R -> [1 ... 4]Ḋ -> [2, 3, 4]       | Range [2 ... n]   |
-----------------------------------------------------------------------------------------
| Ṗ       | Pop from list     | 4Ṗ -> [1 ... 4]Ṗ -> [1, 2, 3]       | Range [1 ... n-1] |
-----------------------------------------------------------------------------------------
| Ẇ       | Sublists of list  | 4Ẇ -> [1 ... 4]Ẇ                    | All sublists of R |
|         |                   | -> [[1], [2], [3], [4], [1, 2],     |                   |
|         |                   |     [2, 3], [3, 4], [1, 2, 3],      |                   |
|         |                   |     [2, 3, 4], [1, 2, 3, 4]]        |                   |
-----------------------------------------------------------------------------------------
| Ẋ       | Shuffle list      | 4Ẋ -> [1 ... 4]Ẋ -> [2, 1, 3, 4]    | Shuffles R        |
-----------------------------------------------------------------------------------------
| Œ!      | All permutations  | 3Œ! -> [1, 2, 3]Œ!                  | All permutations  |
|         | of a list         | -> [[1, 2, 3], [1, 3, 2],           | of R              |
|         |                   |     [2, 1, 3], [2, 3, 1],           |                   |
|         |                   |     [3, 1, 2], [3, 2, 1]]           |                   |
-----------------------------------------------------------------------------------------
| ŒḄ      | Non-vectorized    | 4ŒḄ -> [1 ... 4]ŒḄ                  | Bounces R         |
|         | bounce,           | -> [1, 2, 3, 4, 3, 2, 1]            |                   |
|         | z[:-1] + z[::-1]  |                                     |                   |
-----------------------------------------------------------------------------------------
| Œc      | Unordered pairs   | 4Œc -> [1 ... 4]Œc                  | Unordered pairs   |
|         | of a list         | -> [[1, 2], [1, 3], [1, 4], [2, 3], | of R              |
|         |                   |     [2, 4], [3, 4]]                 |                   |
-----------------------------------------------------------------------------------------
| Œċ      | Unordered pairs   | 4Œċ -> [1 ... 4]Œċ                  | Unordered pairs   |
|         | with replacement  | -> [[1, 1], [1, 2], [1, 3], [1, 4], | with replacement  |
|         | of a list         |     [2, 2], [2, 3], [2, 4], [3, 3], | of R              |
|         |                   |     [3, 4], [4, 4]]                 |                   |
-----------------------------------------------------------------------------------------
| ŒP      | Powerset of       | 3ŒP -> [1 ... 3]                    | Powerset of R     |
|         | a list            | -> ['', [1], [2], [3], [1, 2],      |                   |
|         |                   |     [1, 3], [2, 3], [1, 2, 3]]      |                   |
-----------------------------------------------------------------------------------------
| Œp      | Cartesian         | 4,2Œp -> [[1 ... 4], [1 ... 2]]Œp   | Cartesian product |
|         | product of z's    | -> [[1, 1], [1, 2], [2, 1], [2, 2], | of [1 ... z[i]]   |
|         | items             |     [3, 1], [3, 2], [4, 1], [4, 2]] | for i in z        |
-----------------------------------------------------------------------------------------

Czasami warto czytać ze standardowego wejścia, gdy są dokładnie dwa wejścia

Galaretka jest zoptymalizowana do pobierania danych wejściowych z argumentów wiersza poleceń. Jednak jest również zoptymalizowany do pisania monad, a nie diad; z diadami istnieje tyle możliwych znaczeń dla każdego wbudowanego, że często trzeba wydawać postacie, aby ujednoznacznić, podczas gdy z diadami jest zwykle wiele sposobów na wypowiedzenie tego samego.

Jako takie, jeśli używasz jednego z dwóch wejść tylko raz, a problem jest taki, że nie mogą być łatwo odczytane z niejawnie ⁴(tj albo trzeba sprawić, że ⁴wyraźne, albo wydać na charakter }, @lub tym podobne) , rozważ odczytanie go ze standardowego wejścia Ɠzamiast umieszczania go w wierszu poleceń; pozwala to precyzyjnie umieścić dane wejściowe dokładnie tam, gdzie są potrzebne, poprzez umieszczenie Ɠdanych wejściowych, zapewniając jednocześnie, że wszelkie inne dane wejściowe będą pobierane z innych danych wejściowych. To kosztuje bajt i oszczędza bajt, a w zależności od problemu może zaoszczędzić drugi bajt, dając więcej możliwości zmiany kolejności kodu.

Istnieje kilka nieoczywistych sposobów sprawdzania właściwości argumentu za pomocą Ƒ. Poniżej kilka. Wyszedłem na zewnątrz mnóstwo zastosowań tego szybkiego (np AƑ, ŒuƑ, 3Ƒ), ponieważ są one już najprostsze sposoby osiągania ich zachowanie.

OƑ  Is number?
ỌƑ  Is character? (errors on negative numeric input)
ḂƑ  Between 0 and 2? 0<=x<2 (python). <2aAƑƊ or of course ⁼Ḃ$ in Jelly.
ḞƑ  Is integer?
UƑ  Like `ŒḂ`, but checks if all sublists of depth 1 are palindromes.
ṠƑ  Is one of -1, 0, 1? (e-r1¤$)

Edytuj to, aby dodać więcej interesujących skrzynek.

Możesz wypróbować edytor online Jelly Balls zaprojektowany do łatwego budowania kodu w języku Jelly .

Funkcje obejmują:

• Paleta poleceń ze wszystkimi atomami i znakami składni uporządkowanymi według typu
• Analizator składni online rozpoznający literały i 2-bajtowe atomy w kodzie
• Uproszczony interpreter Jelly w przeglądarce do uruchamiania kodu Jelly na stronie internetowej w javascript
• Bezpośrednie linki do przeniesienia kodu do TIO lub innej sesji Jelly Balls
• Automatyczne podpowiedzi
• Zoptymalizowany dla urządzeń mobilnych

Spróbuj: https://jellyballs.github.io

• Szczegółowy raport śledzenia przedstawiający argumenty i wyniki każdego wykonanego kroku

• Raport kodu pokazujący opis każdego kroku

• Strona przepisów z przykładami galaretki

• Interaktywna strona kodowa zawierająca 256 galaretowych znaków