Problem można rozwiązać w O (polilog (b)).
Definiujemy f(d, n)liczbę całkowitą do d cyfr dziesiętnych z sumą cyfr mniejszą lub równą n. Można zauważyć, że tę funkcję pełni formuła

Wyprowadźmy tę funkcję, zaczynając od czegoś prostszego.
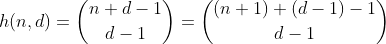
Funkcja h zlicza liczbę sposobów wyboru d - 1 elementów z zestawu wielu zawierającego n + 1 różnych elementów. Jest to także liczba sposobów podziału n na przedziały d, które można łatwo zobaczyć, budując d - 1 ogrodzenie wokół n i sumując każdą oddzielną sekcję. Przykład dla n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
Zatem h zlicza wszystkie liczby posiadające sumę cyfr cyfr nid. Tyle że działa tylko dla n mniej niż 10, ponieważ cyfry są ograniczone do 0 - 9. Aby to naprawić dla wartości 10–19, musimy odjąć liczbę partycji mających jeden pojemnik z liczbą większą niż 9, którą od tej pory będę nazywał przepełnione pojemniki.
Termin ten można obliczyć, ponownie wykorzystując h w następujący sposób. Bieżemy liczbę sposobów podziału n-10, a następnie wybieramy jeden z pojemników, w które należy wstawić 10, co powoduje, że liczba partycji ma jeden przepełniony pojemnik. Wynikiem jest następująca funkcja wstępna.
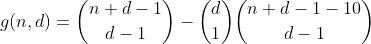
Kontynuujemy tę drogę dla n mniejszej lub równej 29, licząc wszystkie sposoby podziału n - 20, a następnie wybierając 2 pojemniki, w których umieszczamy 10, licząc w ten sposób liczbę partycji zawierających 2 przepełnione pojemniki.
Ale w tym momencie musimy być ostrożni, ponieważ już policzyliśmy partycje posiadające 2 przepełnione kosze w poprzednim okresie. Nie tylko to, ale faktycznie policzyliśmy je dwa razy. Użyjmy przykładu i spójrzmy na partycję (10,0,11) z sumą 21. W poprzednim okresie odjęliśmy 10, obliczyliśmy wszystkie partycje pozostałych 11 i umieściliśmy 10 w jednym z 3 przedziałów. Ale do tej konkretnej partycji można dotrzeć na dwa sposoby:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
Ponieważ te partycje policzyliśmy również raz w pierwszym semestrze, całkowita liczba partycji z 2 przepełnionymi pojemnikami wynosi 1 - 2 = -1, więc musimy je policzyć jeszcze raz, dodając następny termin.
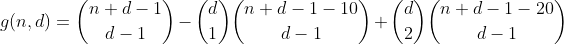
Myśląc o tym trochę więcej, wkrótce odkrywamy, że liczba razy, w której partycja z określoną liczbą przepełnionych pojemników jest liczona w określonym terminie, może być wyrażona w poniższej tabeli (kolumna i reprezentuje termin i, partycje j wiersza z przepełnieniem j pojemniki).
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
Tak, to trójkąt paskalowy. Interesuje nas tylko liczba w pierwszym rzędzie / kolumnie, czyli liczba partycji z zerowymi przepełnionymi pojemnikami. A ponieważ na przemian suma każdego rzędu, ale pierwszy równa się 0 (np. 1 - 4 + 6 - 4 + 1 = 0), w ten sposób pozbywamy się ich i dochodzimy do przedostatniej formuły.
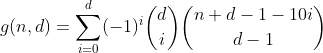
Ta funkcja zlicza wszystkie liczby z cyframi d o sumie cyfr n.
A co z liczbami o sumie cyfr mniejszej niż n? Możemy zastosować standardową powtarzalność dla dwumianów plus argument indukcyjny, aby to pokazać
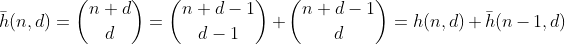
zlicza liczbę partycji z cyfrą co najwyżej n. I z tego można uzyskać f przy użyciu tych samych argumentów, co dla g.
Korzystając z tego wzoru, możemy na przykład znaleźć liczbę liczb ciężkich w przedziale od 8000 do 8999 1000 - f(3, 20), ponieważ, ponieważ w tym przedziale jest tysiąc liczb, i musimy odjąć liczbę liczb z sumą cyfr mniejszą lub równą 28 jednocześnie przyjmując do wiadomości, że pierwsza cyfra już stanowi 8 w sumie cyfr.
Jako bardziej złożony przykład przyjrzyjmy się liczbie ciężkich liczb w przedziale 1234..5678. Możemy najpierw przejść od 1234 do 1240 w krokach 1. Następnie przechodzimy od 1240 do 1300 w krokach 10. Powyższa formuła podaje nam liczbę ciężkich liczb w każdym takim przedziale:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
Teraz przechodzimy od 1300 do 2000 w krokach co 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
Od 2000 do 5000 w krokach co 1000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
Teraz musimy ponownie zmniejszyć rozmiar kroku, przechodząc z 5000 do 5600 w krokach co 100, z 5600 do 5670 w krokach co 10, a na koniec z 5670 do 5678 w krokach co 1.
Przykładowa implementacja Pythona (która tymczasem otrzymała niewielkie optymalizacje i testy):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
Edycja : zastąpiono kod zoptymalizowaną wersją (która wygląda jeszcze brzydiej niż kod oryginalny). Naprawiłem również kilka narożnych skrzynek, gdy byłem przy tym. heavy(1234, 100000000)trwa około milisekundy na moim komputerze.
