27

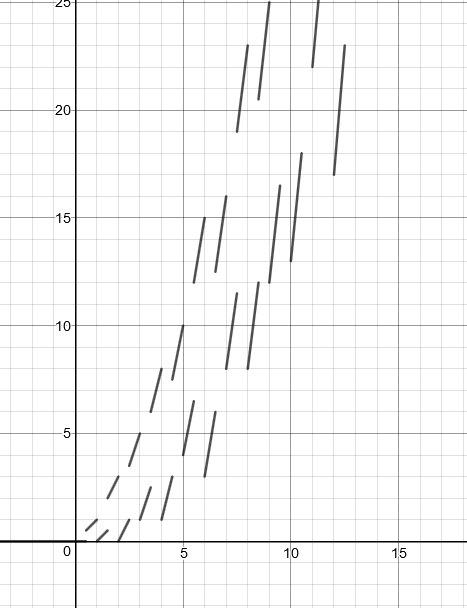
Nazywam tę sekwencję „sekwencją Jezusa”, ponieważ jest to suma modów . </pun>

Dla tej sekwencji bierzesz wszystkie dodatnie liczby całkowite m mniejsze niż wejściowe n i sumę n modulo każdego m . Innymi słowy:

a_{n} = \sum_{m = 1}^{n - 1} n mod m

$a_n = \sum_{m=1}^{n-1}{n\bmod m}$

Na przykład weźmy termin 14 :

14 % 1 = 0
14 % 2 = 0
14 % 3 = 2
14 % 4 = 2
14 % 5 = 4
14 % 6 = 2
14 % 7 = 0
14 % 8 = 6
14 % 9 = 5
14 % 10 = 4
14 % 11 = 3
14 % 12 = 2
14 % 13 = 1
0+0+2+2+4+2+0+6+5+4+3+2+1=31

Twoim celem jest napisanie funkcji, która implementuje tę sekwencję. Powinieneś wziąć termin sekwencji (będzie to dodatnia liczba całkowita od 1 do 2 ³¹ ) jako jedyne wejście i wyprowadzić wartość tego terminu. To jest OEIS A004125 .

Jak zawsze obowiązują standardowe luki i wygrywa najkrótsza odpowiedź w bajtach!

code-golf sequence division

— Nissa
źródło

7

05AB1E , 3 bajty

L%O

Wypróbuj online!

— Pan Xcoder
źródło

8

Haskell , 22 bajty

f x=sum$mod x<$>[1..x]

Wypróbuj online!

Wyjaśnienie

Tak.

— ბიმო
źródło

5

Świetne wyjaśnienie

— Esolanging Fruit

7

Rubin , 28 27 23 bajtów

-4 bajty dzięki @daniero.

->n{(1..n).sum{|i|n%i}}

Wypróbuj online!

Rubinowy, 28 bajtów

f=->n{n>($.+=1)?n%$.+f[n]:0}

Wypróbuj online!

— Jordania
źródło

6

Funky , 25 bajtów

n=>fors=~-i=1i<n)s+=n%i++

Wydaje się, że tylko naiwna odpowiedź działa.

Wypróbuj online!

Desmos , 25 bajtów.

f(x)=\sum_{n=1}^xmod(x,n)

Wklej do Desmos, a następnie uruchom go, dzwoniąc f.

Po wklejeniu do Desmos lateks wygląda tak

Wykres jednak wygląda

Chociaż wygląda to losowo i wszędzie, jest to wynik tylko obsługi liczb całkowitych.

RProgN 2 , 9 bajtów

x=x³x\%S+

Wyjaśnił

x=x³x\%S+
x=          # Store the input in "x"
  x         # Push the input to the stack.
   ³x\%     # Define a function which gets n%x
       S    # Create a stack from "x" with the previous function. Thus this gets the range from (1,x), and runs (i%x) on each element.
        +   # Get the sum of this stack.

Wypróbuj online!

ReRegex , 71 bajtów

#import math
(_*)_a$/d<$1_>b$1a/(\d+)b/((?#input)%$1)+/\+a//u<#input
>a

Wypróbuj online!

ARBLE , 19 bajtów

sum(range(1,a)|a%i)

Wypróbuj online!

Może później 56 bajtów

whenf is*{n=0whenx is*{ifx>0{n=n+f%x x--}elseprintn}x=f}

Wypróbuj online!

— ATaco
źródło

Czy zgłoszenia do tego wyzwania kiedykolwiek się zakończą? Do tej pory dostawałem nowy co 40 minut: P

— Nissa

@StephenLeppik Oh Nadal mam więcej, nie martw się.

— ATaco,

@StephenLeppik Wolałbym nie, ponieważ są różnej jakości w różnych językach.

— ATaco,

@StephenLeppik Połączyłem je dla ciebie, niechętnie.

— ATaco,

4

Proszę nie rób tego. Oddzielne języki - nawet osobne podejścia - powinny zawierać osobne odpowiedzi.

— Dennis,

5

Galaretka , 3 bajty

%RS

Wyjaśnienie

%RS
 R   Range(input)  [1...n]
%    Input (implicit) modulo [1...n]->[n%1,n%2...n%n]
  S  Sum of the above

Wypróbuj online!

— dylnan
źródło

5

MATL , 4 bajty

t:\s

Wypróbuj online!

Wyjaśnienie:

t      % Duplicate input. Stack: {n, n}
 :     % Range 1...n. Stack: {n, [1...n]}
  \    % Modulo. Stack: {[0,0,2,2,4,...]}
   s   % Sum. Implicitly display result.

— Sanchises
źródło

4

Ohm v2 , 4 bajty

D@%Σ

Wypróbuj online!

— Cinaski
źródło

4

R, 20 bajtów

sum((n=scan())%%1:n)

Wypróbuj online!

— plannapus
źródło

4

Python 2 , 44 bajty

lambda n:sum(map(lambda x:x%(n-x),range(n)))

Wypróbuj online!

EDYCJA: Zmieniono zakres (0, n) na zakres (n)

— Max00355
źródło

2

Witam i witam na stronie! rangedomyślnie bierze pierwszy argument 0, więc możesz to skrócić o dwa bajty, robiąc range(n)zamiast tego.

— DJMcMayhem

Och wow! Nawet o tym nie myślałem. Dzięki

— Max00355,

1

Witamy w PPCG! Możesz użyć rozumienia listy zamiast map38 bajtów: Wypróbuj online!

— Pan Xcoder,

Masz rację, ale wykorzystano to w odpowiedzi Neila, więc nie byłem pewien, czy skopiowanie go byłoby najlepsze. Chyba, że coś mi tu brakuje. Chciałem opublikować alternatywę, nawet jeśli była ona nieco dłuższa.

— Max00355,

3

JavaScript (ES6), 26 bajtów

f=(n,k=n)=>n&&k%n+f(n-1,k)

Próbny

Pokaż fragment kodu

f=(n,k=n)=>n&&k%n+f(n-1,k)

for(n = 1; n < 30; n++) {
  console.log('a(' + n + ') = ' + f(n))
}

Rozwiń fragment kodu

— Arnauld
źródło

3

Python 3 , 37 bajtów

lambda a:sum(a%k for k in range(1,a))

Wypróbuj online!

— Neil
źródło

4 odpowiedzi w 10 minut? Łał.

— Nissa,

1

Musi to być bardzo utalentowany programista. ;)

— Neil

3

Węgiel , 9 bajtów

ＩΣＥＮ﹪Ｉθ⊕ι

Wypróbuj online!

Link jest do pełnej wersji kodu:

Print(Cast(Sum(Map(InputNumber(),Modulo(Cast(q),++(i))))));

— Charlie
źródło

3

Standardowy ML (MLton) , 53 51 bajtów

fn& =>let fun f 1a=a|f%a=f(% -1)(a+ &mod%)in f&0end

Wypróbuj online!

Nie golfowany:

fn n =>
   let fun f 1 a = a
         | f x a = f (x-1) (a + n mod x)
   in  
       f n 0
   end

Poprzednia 53 bajtowa wersja:

fn n=>foldl op+0(List.tabulate(n-1,fn i=>n mod(i+1)))

Wypróbuj online!

Wyjaśnienie:

List.tabulateprzyjmuje liczbę całkowitą xi funkcję fi generuje listę [f 0, f 1, ..., f(x-1)]. Biorąc pod uwagę pewną liczbę n, wywołujemy List.tabulatez n-1i funkcję, fn i=>n mod(i+1)aby uniknąć dzielenia przez zero. Wynikowa lista jest sumowana foldl op+0.

— Laikoni
źródło

3

Java (OpenJDK 8) , 45 bajtów

n->{int m=n,s=0;for(;m-->1;)s+=n%m;return s;}

Wypróbuj online!

— Olivier Grégoire
źródło

1

+1 Za użycie -->operatora idzie do ( ).

— raznagul

3

Mathematica , 18 bajtów

#~Mod~i~Sum~{i,#}&

Wypróbuj online!

— całkowicie ludzki
źródło

2

te same bajtyTr[#~Mod~Range@#]&

— J42161217,

3

APL (Dyalog) , 5 bajtów

+/⍳|⊢

Wypróbuj online!

W jaki sposób?

Pociąg monadyczny -

+/ - suma

⊢ - n

| - wektoryzowany moduł

⍳ - zakres n

— Uriel
źródło

3

Japt , 6 5 bajtów

Zaoszczędzono 1 bajt dzięki @Shaggy

Æ%XÃx

Przetestuj online!

Jak to działa

         Implicit: U = input number
Æ        Create the range [0, U),
 %XÃ       mapping each item X to U%X. U%0 gives NaN.
    x    Sum, ignoring non-numbers.
         Implicit: output result of last expression

— ETHprodukcje
źródło

2

05AB1E , 6 bajtów

ÎGIN%+

Wypróbuj online!

Mój pierwszy program 05AB1E;)

~~Przy okazji dostałem dwa 39s, 1 dla JS6 i 1 dla Pythona, ale spóźniłem się~~

Wyjaśnienie:

ÎGIN%+
Î                      # Push 0, then input, stack = [(accumulator = 0), I]
 G                     # For N in range(1, I), stack = [(accumulator)]
  IN                   # Push input, then N, stack = [(accumulator), I, N]
    %                  # Calculate I % N, stack = [(accumulator), I % N]
     +                 # Add the result of modulus to accumulator

— Shieru Asakoto
źródło

2

Rubinowy , 23 bajty

->n{(1..n).sum{|i|n%i}}

Wypróbuj online!

— GB
źródło

2

Julia 0,4, 15 bajtów

x->sum(x%[1:x])

Wypróbuj online!

— Lescurel
źródło

2

Dodaj ++ , 14 bajtów

L,RAdx$p@BcB%s

Wypróbuj online!

Jak to działa

L,   - Create a lambda function.
     - Example argument:     [7]
  R  - Range;        STACK = [[1 2 3 4 5 6 7]]
  A  - Argument;     STACK = [[1 2 3 4 5 6 7] 7]
  d  - Duplicate;    STACK = [[1 2 3 4 5 6 7] 7 7]
  x  - Repeat;       STACK = [[1 2 3 4 5 6 7] 7 [7 7 7 7 7 7 7]]
  $p - Swap and pop; STACK = [[1 2 3 4 5 6 7] [7 7 7 7 7 7 7]]
  @  - Reverse;      STACK = [[7 7 7 7 7 7 7] [1 2 3 4 5 6 7]]
  Bc - Zip;          STACK = [[7 1] [7 2] [7 3] [7 4] [7 5] [7 6] [7 7]]
  B% - Modulo each;  STACK = [0, 1, 1, 3, 2, 1, 0]
  s  - Sum;          STACK = [8]

— Cairney Coheringaahing
źródło

2

4 , 67 bajtów

4 nie ma wbudowanego żadnego modulo .

3.79960101002029980200300023049903204040310499040989804102020195984

Wypróbuj online!

— Uriel
źródło

2

Windows Batch (CMD), 63 bajty

@set s=0
@for /l %%i in (1,1,%1)do @set/as+=%1%%%%i
@echo %s%

Poprzednia 64-bajtowa wersja:

@set/ai=%2+1,s=%3+%1%%i
@if %i% neq %1 %0 %1 %i% %s%
@echo %s%

— Neil
źródło

2

T-SQL, 80 79 bajtów

-1 bajt dzięki @MickyT

WITH c AS(SELECT @ i UNION ALL SELECT i-1FROM c WHERE i>1)SELECT SUM(@%i)FROM c

Pobiera dane wejściowe z parametru o nazwie integer @, mniej więcej tak:

DECLARE @ int = 14;

Używa wspólnego wyrażenia tabelowego do generowania liczb od 1do n. Następnie używa tego cte do podsumowania modułów.

Uwaga: cte potrzebuje ;między poprzednią instrukcją a cte. Większość kodu, który widziałem, umieszcza ;tuż przed deklaracją, ale w tym przypadku mogę zapisać bajt, umieszczając go w instrukcji wejściowej (ponieważ technicznie sam kod jest jedyną instrukcją).

Wypróbuj (SEDE)

Mniej „SQL-y” to tylko 76 bajtów. Tym razem zmienna wejściowa jest @izamiast @(zapisuje jeden bajt). Ten po prostu wykonuje whilepętlę.

DECLARE @ int=2,@o int=0WHILE @<@i BEGIN SELECT @o+=@i%@,@+=1 END PRINT @o

— Brian J.
źródło

2

PHP , 61 bajtów

-2 bajty do usunięcia tagu zamykającego

<?php $z=fgets(STDIN);for($y=1;$y<$z;$y++){$x+=$z%$y;}echo$x;

Wypróbuj online!

— NK1406
źródło

2

Japt `-mx` , 3 bajty

N%U

Wypróbuj online!

— Luis Felipe De Jesus Munoz
źródło

2

Brachylog , 9 bajtów

⟨gz⟦₆⟩%ᵐ+

Wypróbuj online!

— Kroppeb
źródło

1

Łuska , 5 bajtów

ΣṠM%ḣ

Wypróbuj online!

Wyjaśnienie

ΣṠM%ḣ  -- implicit input x, example: 5
 ṠM%   -- map (mod x) over the following..
    ḣ  -- ..the range [1..x]: [5%1,5%2,5%3,5%4,5%5] == [0,1,2,1,0]
Σ      -- sum: 0+1+2+1+0 == 4

— ბიმო
źródło

1

Perl 5 , 23 + 1 ( `-p`) = 24 bajty

//;map$\+=$'%$_,1..$_}{

Wypróbuj online!

— Xcali
źródło

1

Pyth , 5 bajtów

s%LQS

s%LQS - Full program, inputs N from stdin and prints sum to stdout
s     - output the sum of
 %LQ  - the function (elem % N) mapped over 
    S - the inclusive range from 1..N

Wypróbuj online!

— Dave
źródło

Och, właściwie znalazłem inne 5 bajtów niż ty, nie przeczytałem twojego poprawnie

— Dave

Podsumowanie modułu

05AB1E , 3 bajty

Haskell , 22 bajty

Wyjaśnienie

Rubin , 28 27 23 bajtów

Rubinowy, 28 bajtów

Funky , 25 bajtów

Desmos , 25 bajtów.

RProgN 2 , 9 bajtów

Wyjaśnił

ReRegex , 71 bajtów

ARBLE , 19 bajtów

Może później 56 bajtów

Galaretka , 3 bajty

MATL , 4 bajty

Ohm v2 , 4 bajty

R, 20 bajtów

Python 2 , 44 bajty

JavaScript (ES6), 26 bajtów

Próbny

Python 3 , 37 bajtów

Węgiel , 9 bajtów

Standardowy ML (MLton) , 53 51 bajtów

Poprzednia 53 bajtowa wersja:

Java (OpenJDK 8) , 45 bajtów

Mathematica , 18 bajtów

APL (Dyalog) , 5 bajtów

Japt , 6 5 bajtów

Jak to działa

05AB1E , 6 bajtów

Rubinowy , 23 bajty

Julia 0,4, 15 bajtów

Dodaj ++ , 14 bajtów

Jak to działa

4 , 67 bajtów

Windows Batch (CMD), 63 bajty

T-SQL, 80 79 bajtów

PHP , 61 bajtów

Japt -mx , 3 bajty

Brachylog , 9 bajtów

Łuska , 5 bajtów

Wyjaśnienie

Perl 5 , 23 + 1 ( -p) = 24 bajty

Pyth , 5 bajtów

Japt `-mx` , 3 bajty

Perl 5 , 23 + 1 ( `-p`) = 24 bajty